题目内容
【题目】已知函数![]()
(Ⅰ)若曲线![]() 与直线
与直线![]() 相切,求
相切,求![]() 的值.
的值.
(Ⅱ)若![]() 设
设![]() 求证:
求证:![]() 有两个不同的零点
有两个不同的零点![]() ,且
,且![]() .(
.(![]() 为自然对数的底数)
为自然对数的底数)
【答案】(Ⅰ)![]() (Ⅱ)证明见解析.
(Ⅱ)证明见解析.
【解析】
(Ⅰ)设切点![]() ,由导数的性质可得
,由导数的性质可得![]() 结合切点在函数
结合切点在函数![]() 上,可得
上,可得![]()
(Ⅱ)不妨设![]() ,
,![]() ,则
,则![]() 在
在![]() 上单调递减,由函数零点存在定理可得存在
上单调递减,由函数零点存在定理可得存在![]() ,使得
,使得![]() ,分类讨论有:①当
,分类讨论有:①当![]() 时,在区间
时,在区间![]() 上存在零点
上存在零点![]() ,且
,且![]() .②当
.②当![]() 时,在区间
时,在区间![]() 上必存在零点
上必存在零点![]() ,且
,且![]() .据此即可证得题中的结论.
.据此即可证得题中的结论.
(Ⅰ)设切点![]()
又切点在函数![]() 上,
上,![]() 即
即![]()
![]()
(Ⅱ)不妨设![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,
,
所以必存在![]() ,使得
,使得![]() ,即
,即![]()
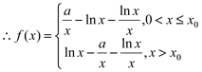 .
.
①当![]() 时,
时,![]() ,
,
所以![]() 在区间
在区间![]() 上单调递减,
上单调递减,
注意到![]() ,
,![]()
所以函数![]() 在区间
在区间![]() 上存在零点
上存在零点![]() ,且
,且![]() .
.
②当![]() 时,
时,![]() 所以
所以![]() 在区间
在区间![]() 上单调递增,
上单调递增,
又![]() ,
,
且![]() ,
,
所以![]() 在区间
在区间![]() 上必存在零点
上必存在零点![]() ,且
,且![]() .
.
综上,![]() 有两个不同的零点
有两个不同的零点![]() 、
、![]() ,且
,且![]() .
.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
【题目】二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
| … | 5 | 0 | -3 | -4 | -3 | m | … |
(1)m= ;
(2)在图中画出这个二次函数的图象;
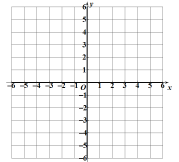
(3)当![]() 时,x的取值范围是 ;
时,x的取值范围是 ;
(4)当![]() 时,y的取值范围是 .
时,y的取值范围是 .