Question

在正三棱柱ABC-A₁B₁C₁（底面是正三角形的直棱柱）中，AA₁=1，AB=

2

，AB₁与BC₁所成的角为（　　）

• A、

  π

  2

• B、

  π

  4

• C、

  π

  3

• D、

  π

  2

Answer 1

考点：异面直线及其所成的角

专题：计算题,空间角,空间向量及应用

分析：分别取A₁C₁，AC的中点E，F，并连接EF，B₁E，则可分别以EB₁，EC₁，EF所在直线为x轴，y轴，z轴建立空间直角坐标系，然后求出向量

AB1

，

BC1

的坐标，从而求出这两向量的夹角，从而求出对应的两异面直线所成角的正弦值．

解答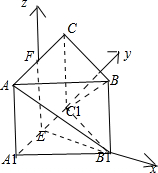： 解：如图，取A₁C₁中点E，AC中点F，并连接EF，
则EB₁，EC₁，EF三条直线两两垂直，
则分别以这三条直线为x轴，y轴，z轴建立如图所示空间直角坐标系；
则有A（0，-

2

2

，1），B₁（

6

2

，0，0），B（

6

2

，0，1），
C₁（0，

2

2

，0）
∴

AB1

=（

6

2

，

2

2

，-1），

BC1

=（-

6

2

，

2

2

，-1），
∴

AB1

•

BC1

=

6

2

×(-

6

2

)+

2

2

×

2

2

+1=0；
∴

AB1

⊥

BC1

，
∴异面直线AB₁和BC₁所成角为90°，
故选：D．

点评：本题主要考查异面直线所成角的求法，以及用向量法求异面直线所成角的方法，考查运算能力，属于基础题．