题目内容
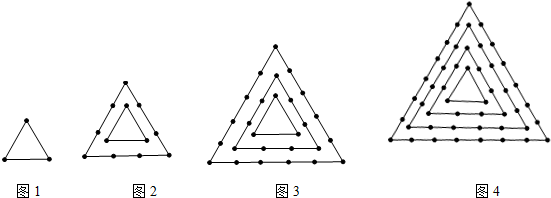
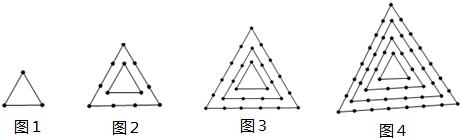
下面四个图案,都是由小正三角形构成,设第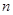 个图形中有
个图形中有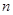 个正三角形中所有小正三角形边上黑点的总数为
个正三角形中所有小正三角形边上黑点的总数为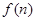 .
.
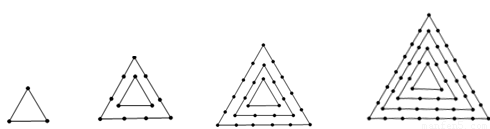
图1 图2 图3 图4
(Ⅰ)求出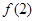 ,
,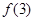 ,
,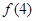 ,
,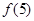 ;
;
(Ⅱ)找出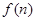 与
与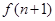 的关系,并求出
的关系,并求出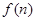 的表达式;
的表达式;
(Ⅲ)求证: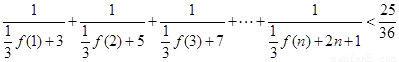 (
(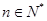 ).
).
【答案】
(Ⅰ)12,27,48,75.
(Ⅱ)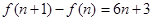 ,
,
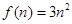 .(Ⅲ)详见解析.
.(Ⅲ)详见解析.
【解析】
试题分析:(Ⅰ)求出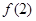 ,
,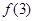 ,
,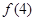 ,
,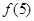 ,第二个图形的黑点个数为第一个图形的黑点个数加上外面的三角形上的黑点个数,即
,第二个图形的黑点个数为第一个图形的黑点个数加上外面的三角形上的黑点个数,即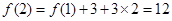 ,第三个图形的黑点个数为第二个图形的黑点个数加上外面的三角形上的黑点个数,即
,第三个图形的黑点个数为第二个图形的黑点个数加上外面的三角形上的黑点个数,即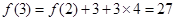 ,以此类推可求出
,以此类推可求出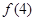 ,
,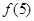 ;(Ⅱ)观察
;(Ⅱ)观察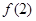 ,
,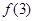 ,
,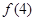 ,
,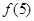 可得到,后一个图形的黑点个数是前一个图形外多加一个三角形,而且每一条边都比内一个三角形多两个黑点,即
可得到,后一个图形的黑点个数是前一个图形外多加一个三角形,而且每一条边都比内一个三角形多两个黑点,即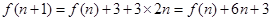 ,即
,即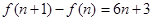 ,求出
,求出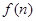 的表达式,像这种关系可用叠加法,即写出
的表达式,像这种关系可用叠加法,即写出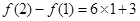 ,
,
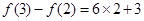 ,
, ,
, ,
,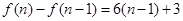 ,把这
,把这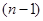 个式子叠加,即可得出
个式子叠加,即可得出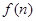 的表达式;(Ⅲ)求证:
的表达式;(Ⅲ)求证: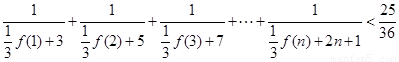 (
(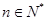 ),
先求出
),
先求出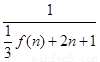 的关系式,得
的关系式,得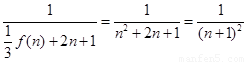 ,由于求证的不等式右边是常数,可考虑利用放缩法,即
,由于求证的不等式右边是常数,可考虑利用放缩法,即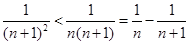 ,这样既可证明.
,这样既可证明.
试题解析:(Ⅰ)由题意有,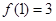 ,
, 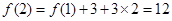 ,
, 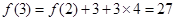 ,
,
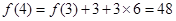 ,
,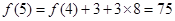 .
.
(Ⅱ)由题意及(Ⅰ)知,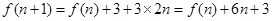 ,
,
即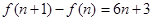 ,所以
,所以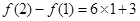 ,
,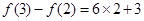 ,
, ,
,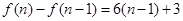 ,
5分
,
5分
将上面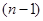 个式子相加,得:
个式子相加,得: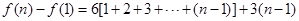
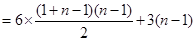
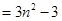 6分
6分
又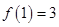 ,所以
,所以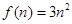 .
7分
.
7分
(Ⅲ)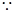
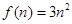 ,∴
,∴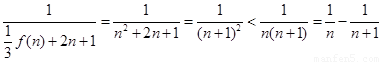 . 9分
. 9分
当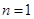 时,
时,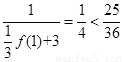 ,原不等式成立. 10分
,原不等式成立. 10分
当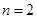 时,
时,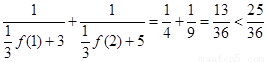 ,原不等式成立. 11分
,原不等式成立. 11分
当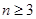 时,
时,
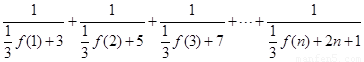
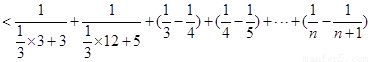
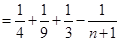
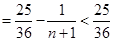 ,
原不等式成立.
13分
,
原不等式成立.
13分
综上所述,对于任意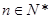 ,原不等式成立. 14分
,原不等式成立. 14分
考点:归纳推理,放缩法证明不等式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目




 (
(



 (
(



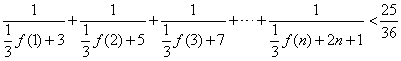 (
(