题目内容
下面四个图案,都是由小正三角形构成,设第n个图形中有n个正三角形中所有小正三角形边上黑点的总数为f(n).
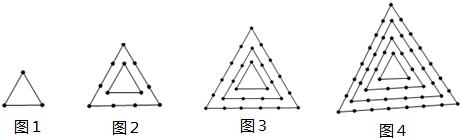
(1)求出f(2),f(3),f(4),f(5);
(2)找出f(n)与f(n+1)的关系,并求出f(n)的表达式.

(1)求出f(2),f(3),f(4),f(5);
(2)找出f(n)与f(n+1)的关系,并求出f(n)的表达式.
分析:(1)根据条件分别求出f(2),f(3),f(4),f(5)即可;
(2)根据条件找出f(n)与f(n+1)的关系,利用累加法即可求出f(n)的表达式.
(2)根据条件找出f(n)与f(n+1)的关系,利用累加法即可求出f(n)的表达式.
解答:解:(1)由题意有f(1)=3,
f(2)=f(1)+3+3×2=12,
f(3)=f(2)+3+3×4=27,
f(4)=f(3)+3+3×6=48,
f(5)=f(4)+3+3×8=75.
(2)由题意及(1)知,f(n+1)=f(n)+3+3×2n=f(n)+6n+3,
即f(n+1)-f(n)=6n+3,
所以f(2)-f(1)=6×1+3,
f(3)-f(2)=6×2+3,
f(4)-f(3)=6×3+3,
…
f(n)-f(n-1)=6(n-1)+3,
将上面(n-1)个式子相加,
得:f(n)-f(1)=6[1+2+3+…+(n-1)]+3(n-1)=6×
+3(n-1)=3n2-3
又f(1)=3,
所以f(n)=3n2.
故答案为:(1)12,27,48,75.
(2)f(n+1)-f(n)=6n+3,f(n)=3n2.
f(2)=f(1)+3+3×2=12,
f(3)=f(2)+3+3×4=27,
f(4)=f(3)+3+3×6=48,
f(5)=f(4)+3+3×8=75.
(2)由题意及(1)知,f(n+1)=f(n)+3+3×2n=f(n)+6n+3,
即f(n+1)-f(n)=6n+3,
所以f(2)-f(1)=6×1+3,
f(3)-f(2)=6×2+3,
f(4)-f(3)=6×3+3,
…
f(n)-f(n-1)=6(n-1)+3,
将上面(n-1)个式子相加,
得:f(n)-f(1)=6[1+2+3+…+(n-1)]+3(n-1)=6×
| (1+n-1)(n-1) |
| 2 |
又f(1)=3,
所以f(n)=3n2.
故答案为:(1)12,27,48,75.
(2)f(n+1)-f(n)=6n+3,f(n)=3n2.
点评:本题主要考查归纳推理的应用,利用累加法求出f(n)是解决本题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目




 (
(



 (
(



 (
(