题目内容
已知坐标平面上三点A(2,0),B(0,2),C(cosα,sinα).
(1)若(
+
)2=7(O为原点),求向量
与
夹角的大小;
(2)若
⊥
,求sin2α的值.
(1)若(
| OA |
| OC |
| OB |
| OC |
(2)若
| AC |
| BC |
(1)∵
+
=(2+cosα,sinα),(
+
)2=7,
∴(2+cosα)2+sin2α=7,
∴cosα=
.
又B(0,2),C(cosα,sinα),设
与
的夹角为θ,
则:cosθ=
=
=sinα=±
,
∴
与
的夹角为
或
π.
(2)∵
=(cosα-2,sinα),
=(cosα,sinα-2),
由
⊥
,∴
•
=0,
可得cosα+sinα=
,①
∴(cosα+sinα)2=
,∴2sinαcosα=-
,sin2α=-
| OA |
| OC |
| OA |
| OC |
∴(2+cosα)2+sin2α=7,
∴cosα=
| 1 |
| 2 |
又B(0,2),C(cosα,sinα),设
| OB |
| OC |
则:cosθ=
| ||||
|
|
| 2sinα |
| 2 |
| ||
| 2 |
∴
| OB |
| OC |
| π |
| 6 |
| 5 |
| 6 |
(2)∵
| AC |
| BC |
由
| AC |
| BC |
| AC |
| BC |
可得cosα+sinα=
| 1 |
| 2 |
∴(cosα+sinα)2=
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
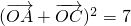 (O为坐标原点),求向量
(O为坐标原点),求向量 与
与 夹角的大小;
夹角的大小; ,当0<α<π时,求tanα的值.
,当0<α<π时,求tanα的值. (O为原点),求向量
(O为原点),求向量 与
与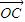 夹角的大小;
夹角的大小; ,求sin2α的值.
,求sin2α的值.