题目内容
11.已知在平面直角坐标系中,$\left\{\begin{array}{l}{x≤2}\\{x+y≥4}\\{x-y≥-2}\end{array}\right.$,表示的平面区域为Ω,O(0,0),A(1,0),若M∈Ω.则$\frac{\overrightarrow{OA}•\overrightarrow{OM}}{|\overrightarrow{OM}|}$的取值范围是[-$\frac{\sqrt{10}}{10}$,$\frac{\sqrt{2}}{2}$].分析 作出不等式组对应的平面区域,利用平面向量的数量积进行转化,利用数形结合进行求解即可.
解答 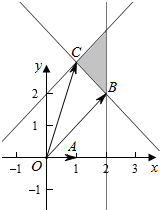 解:$\frac{\overrightarrow{OA}•\overrightarrow{OM}}{|\overrightarrow{OM}|}$=|$\overrightarrow{OA}$|•$\frac{\overrightarrow{OA}•\overrightarrow{OM}}{|\overrightarrow{OM}|•|\overrightarrow{OA}|}$=|$\overrightarrow{OA}$|•cos<$\overrightarrow{OA}$,$\overrightarrow{OM}$>,
解:$\frac{\overrightarrow{OA}•\overrightarrow{OM}}{|\overrightarrow{OM}|}$=|$\overrightarrow{OA}$|•$\frac{\overrightarrow{OA}•\overrightarrow{OM}}{|\overrightarrow{OM}|•|\overrightarrow{OA}|}$=|$\overrightarrow{OA}$|•cos<$\overrightarrow{OA}$,$\overrightarrow{OM}$>,
作出不等式组对应的平面区域如图:
由图象知当M位于B时$\overrightarrow{OA}$,$\overrightarrow{OM}$的夹角最小,
当M位于C时$\overrightarrow{OA}$,$\overrightarrow{OM}$的夹角最大,
由$\left\{\begin{array}{l}{x=2}\\{x+y=4}\end{array}\right.$,即$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,此时B(2,2),则cos<$\overrightarrow{OA}$,$\overrightarrow{OM}$>=$\frac{\sqrt{2}}{2}$,
由$\left\{\begin{array}{l}{x+y=4}\\{x-y=-2}\end{array}\right.$,即$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$,此时C(1,3),则cos<$\overrightarrow{OA}$,$\overrightarrow{OM}$>=$\frac{1}{\sqrt{{1}^{2}+{3}^{2}}}$=$\frac{1}{\sqrt{10}}$=$\frac{\sqrt{10}}{10}$,
故-$\frac{\sqrt{10}}{10}$≤cos<$\overrightarrow{OA}$,$\overrightarrow{OM}$>≤$\frac{\sqrt{2}}{2}$,
即-$\frac{\sqrt{10}}{10}$≤$\frac{\overrightarrow{OA}•\overrightarrow{OM}}{|\overrightarrow{OM}|}$≤$\frac{\sqrt{2}}{2}$,
故答案为:[-$\frac{\sqrt{10}}{10}$,$\frac{\sqrt{2}}{2}$]
点评 本题主要考查线性规划的应用,利用平面向量的数量积进行转化以及利用数形结合是解决本题的关键.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案| A. | 2-$\frac{1}{{2}^{n}}$ | B. | 1-$\frac{1}{{2}^{n}}$ | C. | 1-$\frac{1}{{2}^{n+1}}$ | D. | $\frac{1}{{2}^{n}}$ |
| A. | [a2,+∞) | B. | (0,a2] | C. | (a2,+∞) | D. | (0,a2) |
 如图,△ABC的内切圆I切AB、BC、AC于点D、E、F.直线EF与AI、BI、DI交于点M、N、K.求证:DM•KE=DN•KF.
如图,△ABC的内切圆I切AB、BC、AC于点D、E、F.直线EF与AI、BI、DI交于点M、N、K.求证:DM•KE=DN•KF. 现有一矩形空地,准备将其划分成六个区域栽种四种不同颜色的花卉进行绿化,要求4、5、6三个区域中的任意两个都不能栽种相同颜色的花卉,而且相邻的两个区域也不能栽种相同的颜色的花卉,则不同的花卉栽种方式有( )
现有一矩形空地,准备将其划分成六个区域栽种四种不同颜色的花卉进行绿化,要求4、5、6三个区域中的任意两个都不能栽种相同颜色的花卉,而且相邻的两个区域也不能栽种相同的颜色的花卉,则不同的花卉栽种方式有( ) 如图,在正四棱锥S-ABCD中,SA=2AB=2,M,N分别是棱SA,SC的中点,平面SBC∩平面SAD=l.
如图,在正四棱锥S-ABCD中,SA=2AB=2,M,N分别是棱SA,SC的中点,平面SBC∩平面SAD=l.