题目内容
已知函数f(x)＝log4(ax2＋2x＋3)．
(1)若f(1)＝1，求f(x)的单调区间；
(2)是否存在实数a，使f(x)的最小值为0？若存在，求出a的值；若不存在，说明理由．
解：(1)∵f(1)＝1，
∴log4(a＋5)＝1，因此a＋5＝4，a＝－1，
这时f(x)＝log4(－x2＋2x＋3)．
由－x2＋2x＋3>0得－1<x<3，函数定义域为(－1,3)．
令g(x)＝－x2＋2x＋3.
则g(x)在(－∞，1)上递增，在(1，＋∞)上递减，
又y＝log4x在(0，＋∞)上递增，
所以f(x)的单调递增区间是(－1,1)，递减区间是(1,3)．
(2)假设存在实数a使f(x)的最小值为0，则h(x)＝ax2＋2x＋3应有最小值1，因此应有
解得a＝
.
故存在实数a＝使f(x)的最小值等于0
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
相关题目
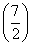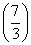<f
<f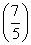
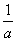，b) B．(10a,1－b)
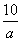，b＋1) D．(a2,2b)
的定义域是________．
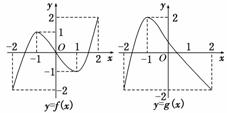
零点的个数为 .