题目内容
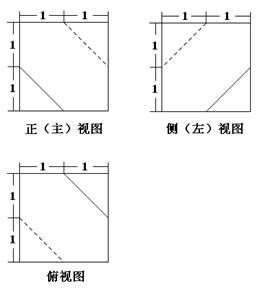
一个几何体的三视图及尺寸如图所示,则该几何体的外接球半径为 ( )
A. | B. | C. | D. |
C
解析试题分析:由三视图可知:该几何体是一个如图所示的三棱锥P-ABC,它是一个正四棱锥P-ABCD的一半,其中底面是一个两直角边都为6的直角三角形,高PE=4.
设其外接球的球心为O,O点必在高线PE上,外接球半径为R,
则在直角三角形BOE中,BO2=OE2+BE2=(PE-EO)2+BE2,
即R2=(4-R)2+(3 )2,解得:R=
)2,解得:R= ,故选C.
,故选C.
考点:三视图,球与多面体的切接问题,空间想象能力

练习册系列答案
相关题目
长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是 ( )
| A.25π | B.50π | C.125π | D.都不对 |
正方体 的面
的面 内有一点
内有一点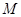 ,满足
,满足 ,则点
,则点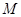 的轨迹是( )
的轨迹是( )
| A.圆的一部分 | B.椭圆的一部分 |
| C.双曲线的一部分 | D.抛物线的一部分 |
若三棱锥的三个侧面两两垂直,且侧棱长均为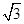 ,则其外接球的表面积为( ).
,则其外接球的表面积为( ).
A.18 | B.36 | C.9 | D. |
某向何体的三视图如图所示,则该几何体的体积为( )
A.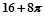 | B.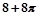 | C.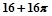 | D.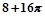 |
 满足
满足

 的最小值.
的最小值.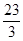
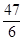
 >
> ,x>y. 求证:
,x>y. 求证: >
> .
. ,
, R.
R. 满足
满足 ,证明:
,证明: 、
、 至少有一个不小于零;
至少有一个不小于零; 、
、 为不相等的正数,且满足
为不相等的正数,且满足 ,求证:
,求证: .
.