题目内容
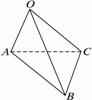
如图所示,在空间四边形ABCD中,已知AC=2,BD=2,E、F分别是AD、BC的中点,且EF=3.求AC和BD所成的角.
解:如图,取CD的中点H,连结EH、HF.
∵E、H分别为AD、CD的中点,
∴EH
AC=
×2=1.
同理,HF
BD=1,
且EH和HF所成的角(或其补角)即为异面直线AC、BD所成的角,不妨设∠EHF=θ.
则cosθ=
,
∴θ=120°.
∴AC、BD所成的角为60°.
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
如图所示，空间四边形ABCD中，AB=BD=AD=2，BC=CD=
| ||
| 2 |
| 3 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
C.
D.
