题目内容
10.平面α内有一以AB为直径的圆,PA⊥α,点C在圆周上移动(不与A,B重合),点D,E分别是A在PC,PB上的射影,则( )| A. | ∠ACD是二面角A-PC-B的平面角 | B. | ∠AED是二面角A-PB-C的平面角 | ||
| C. | ∠EDA是二面角A-PC-B的平面角 | D. | ∠DAE是二面角B-PA-C的平面角 |
分析 利用射影的定义、直径所对的圆周角为直角等知识判定线线垂直,AE⊥PB,AD⊥PC,BC⊥AC.然后利用线线垂直、线面垂直、面面垂直的相互转化关系判定即可.
解答 解:∵PA⊥⊙O所在平面α,BC?α,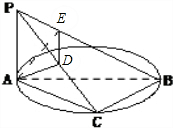
∴PA⊥BC,
∵AB是⊙O的直径,
∴BC⊥AC,
∵PA∩AC=A,
∴BC⊥平面PAC,
∴AD⊥BC,
又∵D是点A在PC上的射影,
∴AD⊥PC,
∵BC∩PC=C,
∴AD⊥平面PBC,
∴AD⊥PB,
又∵AE⊥PB,AD∩AE=A
∴PB⊥面ADE,
∴∠AED是二面角A-PB-C的平面角.
故选:B.
点评 本题考查二面角的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力、推理论证能力,考查化归与转化思想、数形结合思想,是中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
20.在空间直角坐标系Oxyz中,点A(a,a,a),B(a,a,0),C(0,0,a).其中a>0,则△ABC为( )
| A. | 直角三角形 | B. | 等腰直角三角形 | C. | 正三角形 | D. | 钝角三角形 |
1.下列命题中假命题是( )
| A. | ?x,y∈R,使sin(x+y)=sinx+siny成立 | |
| B. | ?x∈R,使(x-1)2≤0成立 | |
| C. | “x+y>2且xy>1”成立的充要条件是x>1且y>1 | |
| D. | ?x∈R,使2x2-2x+1>0成立 |
5.在△ABC中,内角A,B,C的对边分别为a,b,c且a2=b2+c2+bc,则A=( )
| A. | $\frac{2π}{3}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$ |
2.若|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,$\overrightarrow{c}$=2$\overrightarrow{a}$+3$\overrightarrow{b}$,$\overrightarrow{d}$=k$\overrightarrow{a}$-$\overrightarrow{b}$,且$\overrightarrow{c}$⊥$\overrightarrow{d}$,则k=( )
| A. | -b | B. | b | C. | -$\frac{14}{5}$ | D. | $\frac{14}{5}$ |