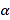题目内容
【题目】如图已知椭圆![]() ,
,![]() 是长轴的一个端点,弦
是长轴的一个端点,弦![]() 过椭圆的中心
过椭圆的中心![]() ,且
,且![]() ,
,![]() .
.
(Ⅰ)求椭圆的方程:
(Ⅱ)设![]() 为椭圆上异于
为椭圆上异于![]() 且不重合的两点,且
且不重合的两点,且![]() 的平分线总是垂直于
的平分线总是垂直于![]() 轴,是否存在实数
轴,是否存在实数![]() ,使得
,使得![]() ,若存在,请求出
,若存在,请求出![]() 的最大值,若不存在,请说明理由.
的最大值,若不存在,请说明理由.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
(Ⅰ)易知![]() 根据条件确定
根据条件确定![]() 形状,即得C坐标,代入椭圆方程可得
形状,即得C坐标,代入椭圆方程可得![]() ,(Ⅱ)即先判断
,(Ⅱ)即先判断![]() 是否成立,设
是否成立,设![]() 的直线方程,与椭圆联立方程组解得
的直线方程,与椭圆联立方程组解得![]() 坐标,根据
坐标,根据![]() 、
、![]() 关系可得
关系可得![]() 坐标,利用斜率坐标公式即得
坐标,利用斜率坐标公式即得![]() 斜率,进而判断
斜率,进而判断![]() 成立,然后根据两点间距离公式计算
成立,然后根据两点间距离公式计算![]() 长度最大值,即可得
长度最大值,即可得![]() 的最大值.
的最大值.
(Ⅰ)∵![]() , ∴
, ∴![]()
又![]() ,即
,即![]() ,2
,2![]()
∴![]() 是等腰直角三角形
是等腰直角三角形
∵![]() , ∴
, ∴![]()
因为点![]() 在椭圆上,∴
在椭圆上,∴![]() ∴
∴![]()
∴所求椭圆方程为![]()
(Ⅱ)对于椭圆上两点![]() 、
、![]() ,∵
,∵![]() 的平分线总是垂直于
的平分线总是垂直于![]() 轴
轴
∴![]() 与
与![]() 所在直线关于
所在直线关于![]() 对称,设
对称,设![]() 且
且![]() ,则
,则![]() ,
,
则![]() 的直线方程
的直线方程![]() ①
①
![]() 的直线方
的直线方![]() ②
②
将①代入![]() 得
得![]() ③
③
∵![]() 在椭圆上,∴
在椭圆上,∴![]() 是方程③的一个根,∴
是方程③的一个根,∴![]()
以![]() 替换
替换![]() ,得到
,得到![]() .
.
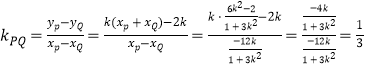
因为![]() ,所以
,所以![]() span>∴
span>∴![]() ∴
∴![]() ,∴存在实数
,∴存在实数![]() ,使得
,使得![]()
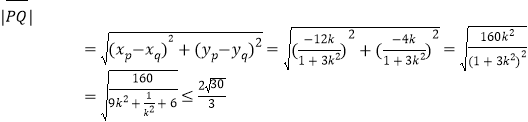
当![]() 时即
时即![]() 时取等号,
时取等号,
又![]() ,
,![]()

练习册系列答案
相关题目