题目内容
【题目】某小区提倡低碳生活，环保出行，在小区提供自行车出租.该小区有40辆自行车供小区住户租赁使用，管理这些自行车的费用是每日92元，根据经验，若每辆自行车的日租金不超过5元，则自行车可以全部出租，若超过5元，则每超过1元，租不出的自行车就增加2辆，为了便于结算，每辆自行车的日租金
元只取整数，用
元表示出租自行车的日纯收入（日纯收入=一日出租自行车的总收入-管理费用）
（1）求函数的解析式及其定义域；
（2）当租金定为多少时，才能使一天的纯收入最大？
【答案】（1）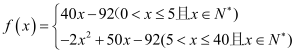
，其定义域为
，（2）定价为12或13，一天的纯收入最大，最大值为220元.
【解析】
试题分析：（1）设日租金为
元（
），当
时，一日出租自行车总收入为
元，则此时
，当
时，一日出租自行车总收入为
，则此时
，因此函数
的为分段函数，则函数
的解析式为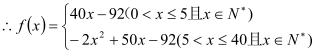
；（2）本问考查求分段函数的最大值，当
且
时，
，函数单调递增，所以当
时
元，当
且时，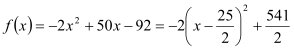 
，根据二次函数图象及性质可知，当
或13时
，因为220>108，所以函数的最大值为220，此时定价为12或13.
试题解析：（1）由题意：当且时，
当且时，
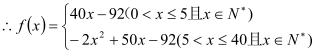
其定义域为
（2）当且时，
当时（元）
当且时，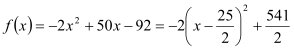
开口向下，对称轴为
，又
当或13时（元）
当租金定为12元或13元时，
一天的纯收入最大为220元
练习册系列答案
阅读快车系列答案
相关题目
