题目内容
(本小题12分)已知二次函数 满足
满足 且
且 .(1)求
.(1)求 的解析式; (2) 当
的解析式; (2) 当 时,不等式:
时,不等式: 恒成立,求实数
恒成立,求实数 的范围.(3)设
的范围.(3)设
 ,求
,求 的最大值;
的最大值;
(1) ;(2)m<-1;(3)
;(2)m<-1;(3) .
.
【解析】
试题分析:(1)由题设 代入
代入 ,根据待定系数法可得
,根据待定系数法可得 ,然后得到函数解析式;(2)由题将问题转化为
,然后得到函数解析式;(2)由题将问题转化为 时,
时, 恒成立问题,即求最值问题,难度不大;(3)由题
恒成立问题,即求最值问题,难度不大;(3)由题 ,根据一元二次函数在给定区间上的单调性进行分类讨论即可得到其最值满足函数.
,根据一元二次函数在给定区间上的单调性进行分类讨论即可得到其最值满足函数.
试题解析:(1)【解析】
令 代入:
代入:
得: ,
,
∴
∴
(2)当 时,
时, 恒成立
恒成立
即: 恒成立;
恒成立;
令 ,
,
则对称轴: ,
,
∴
(3) 
对称轴为:
当 时,即:
时,即: ;如图1:
;如图1:


②当 时,即:
时,即: ;如图2:
;如图2:


综上所述:
考点:待定系数法求函数解析式,恒成立问题,一元二次函数在闭区间上的最值问题

练习册系列答案
相关题目
 的最小值是 .
的最小值是 . = .(
= .( 为虚数单位)
为虚数单位) 与
与 的夹角为
的夹角为 ,
, ,
, ,则
,则 = .
= .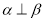 ,
, ,则
,则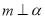
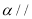
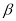 ,
,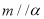 ,则
,则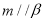
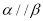 ,
,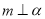 ,则
,则
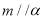 ,
,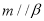 ,则
,则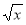 +1)=x+1,则函数f(x)的解析式为( )
+1)=x+1,则函数f(x)的解析式为( )  的最小值为 .
的最小值为 . 经过点
经过点 ,直线
,直线 经过点
经过点
 时,试判断直线
时,试判断直线

 ,试求
,试求 的值.
的值.