题目内容
平面向量 与
与 的夹角为
的夹角为 ,
, ,
, ,则
,则 = .
= .
2
【解析】
试题分析:因为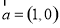 ,所以
,所以 ,所以
,所以
所以

 ,所以答案应填:2.
,所以答案应填:2.
考点:平面向量的数量积.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
题目内容
平面向量 与
与 的夹角为
的夹角为 ,
, ,
, ,则
,则 = .
= .
2
【解析】
试题分析:因为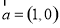 ,所以
,所以 ,所以
,所以
所以

 ,所以答案应填:2.
,所以答案应填:2.
考点:平面向量的数量积.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案