题目内容
9.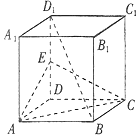 如图,正方体 A BCD-A1 B1C1D1中,E为DD1的中点.
如图,正方体 A BCD-A1 B1C1D1中,E为DD1的中点.(1)证明:BD1⊥AC;
(2)证明:BD1∥平面 ACE.
分析 (1)连结 BD,证明AC⊥BD,AC⊥DD1,推出AC⊥平面 BDD1,然后证明BD1⊥AC.
(2)设AC∩BD=O,连结OE,证明O E∥BD1,然后BD1∥平面ACE.
解答 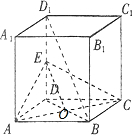 证明:(1)连结 BD,∵四边形ABCD是正方形,
证明:(1)连结 BD,∵四边形ABCD是正方形,
∴AC⊥BD,∵DD1⊥平面ABCD,AC?平面ABCD,
∴AC⊥DD1
∵BD∩DD1=D,BD?平面BDD1,DD1?平面BDD1
∴AC⊥平面 BDD1
∵BD1?平面BDD1
∴BD1⊥AC.
(2)设 AC∩BD=O,连结OE,
∵四边形ABCD是正方形,
∴O是BD的中点∵E为DD1的中点,
∴OE∥BD1
∵OE?平面ACE,BD1?平面ACE,
∴BD1∥平面ACE.
点评 本题考查直线与平面垂直的判定定理的应用,直线与平面平行的判定定理的应用,考查空间想象能力以及逻辑推理能力.

练习册系列答案
相关题目
4.若数列{an}满足(2n+3)an+1-(2n+5)an=(2n+3)(2n+5)lg(1+$\frac{1}{n}$),且a1=5,则数列{$\frac{{a}_{n}}{2n+3}$}的第2016项为( )
| A. | lg2017 | B. | lg2016 | C. | 1+lg2016 | D. | 1+lg2017 |
14.若0<α<2π且cosα≤$\frac{1}{2}$,sinα>$\frac{\sqrt{2}}{2}$,则角α的取值范围是( )
| A. | [$\frac{π}{3}$,$\frac{3}{4}$π) | B. | ($\frac{π}{3}$,$\frac{3}{4}$π] | C. | ($\frac{π}{4}$,$\frac{π}{3}$] | D. | [$\frac{π}{3}$,$\frac{3}{4}$π)∪($\frac{π}{4}$,$\frac{π}{3}$) |
18.如图的等高条形图可以说明的问题是( )
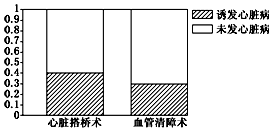

| A. | “心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响是绝对不同的 | |
| B. | “心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响没有什么不同 | |
| C. | 此等高条形图看不出两种手术有什么不同的地方 | |
| D. | “心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响在某种程度上是不同的,但是没有100%的把握 |