题目内容
已知数列{an}满足an+1=
+
,且a1=
,则该数列的前2015项的和等于 .
| 1 |
| 2 |
| an-an2 |
| 1 |
| 2 |
考点:数列递推式,数列的求和
专题:等差数列与等比数列
分析:数列{an}满足an+1=
+
,且a1=
,可得a2=1,a3=
,…,该数列是周期数列,an+2=an.即可得出.
| 1 |
| 2 |
| an-an2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵数列{an}满足an+1=
+
,且a1=
,
∴a2=
+
=1,
a3=
+
=
,
…,
∴该数列是周期数列,an+2=an.
∴该数列的前2015项的和=1007(a1+a2)+a1
=1007×
+
=1511.
故答案为:1511.
| 1 |
| 2 |
| an-an2 |
| 1 |
| 2 |
∴a2=
| 1 |
| 2 |
|
a3=
| 1 |
| 2 |
| 1-12 |
| 1 |
| 2 |
…,
∴该数列是周期数列,an+2=an.
∴该数列的前2015项的和=1007(a1+a2)+a1
=1007×
| 3 |
| 2 |
| 1 |
| 2 |
=1511.
故答案为:1511.
点评:本题考查了数列的周期性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
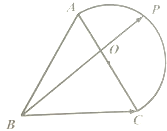 已知△ABC是边长为2的正三角形,以AC为直径作半圆O(如图),P为半圆上任一点,则
已知△ABC是边长为2的正三角形,以AC为直径作半圆O(如图),P为半圆上任一点,则