Question

平面直角坐标系中,若圆的摆线过点(1,0),求这条摆线的参数方程.

Answer 1

思路分析：根据圆的摆线的参数方程的表达式(φ为参数),可知只需求出其中的r，也就是说，摆线的参数方程由圆的半径唯一确定，因此只需把点(1，0)代入参数方程求出r值再代入参数方程的表达式.

解:令r(1-cosφ)=0,可得cosφ=1，

所以φ=2kπ(k∈Z),代入可得x=r(2kπ-sin2kπ)=1.

所以r=.

又根据实际情况可知r是圆的半径，故r＞0.

所以，应有k＞0且k∈Z，即k∈N^*.

所以，所求摆线的参数方程是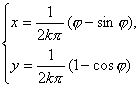(φ为参数)(其中k∈N^*).