题目内容
直线y= x+b能作为下列函数图象的切线的是________(写出所有符合题意的函数的序号)
x+b能作为下列函数图象的切线的是________(写出所有符合题意的函数的序号)
①f(x)= ②f(x)=sinx ③f(x)=x(x2+1)④f(x)=gx.
②f(x)=sinx ③f(x)=x(x2+1)④f(x)=gx.
②④
分析:先求出函数的导函数,然后根据直线y= x+b能作为下列函数图象的切线,根据导数与切线斜率的关系建立等式,看是否成立即可.
x+b能作为下列函数图象的切线,根据导数与切线斜率的关系建立等式,看是否成立即可.
解答:①f′(x)=-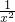 =
= 不成立;
不成立;
②f′(x)=cosx= 可以成立;
可以成立;
③f′(x)=3x2+1= 不成立;
不成立;
④f′(x)=ex= 可成立.
可成立.
故直线y= x+b能作为②④函数图象的切线,
x+b能作为②④函数图象的切线,
故答案为:②④.
点评:本题主要考查了利用导数研究曲线上某点切线方程,关键利用导数与切线斜率的关系,属于基础题.
分析:先求出函数的导函数,然后根据直线y=
 x+b能作为下列函数图象的切线,根据导数与切线斜率的关系建立等式,看是否成立即可.
x+b能作为下列函数图象的切线,根据导数与切线斜率的关系建立等式,看是否成立即可.解答:①f′(x)=-
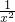 =
= 不成立;
不成立;②f′(x)=cosx=
 可以成立;
可以成立;③f′(x)=3x2+1=
 不成立;
不成立;④f′(x)=ex=
 可成立.
可成立.故直线y=
 x+b能作为②④函数图象的切线,
x+b能作为②④函数图象的切线,故答案为:②④.
点评:本题主要考查了利用导数研究曲线上某点切线方程,关键利用导数与切线斜率的关系,属于基础题.

练习册系列答案
相关题目
 x+b能作为下列函数图象的切线的是 (写出所有符合题意的函数的序号)
x+b能作为下列函数图象的切线的是 (写出所有符合题意的函数的序号)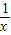 ②f(x)=sinx ③f(x)=x(x2+1)④f(x)=gx.
②f(x)=sinx ③f(x)=x(x2+1)④f(x)=gx.