题目内容
直线y=
x+b能作为下列函数图象的切线的是______(写出所有符合题意的函数的序号)
①f(x)=
②f(x)=sinx ③f(x)=x(x2+1)④f(x)=gx.
| 1 |
| 2 |
①f(x)=
| 1 |
| x |
①f′(x)=-
=
不成立;
②f′(x)=cosx=
可以成立;
③f′(x)=3x2+1=
不成立;
④f′(x)=ex=
可成立.
故直线y=
x+b能作为②④函数图象的切线,
故答案为:②④.
| 1 |
| x 2 |
| 1 |
| 2 |
②f′(x)=cosx=
| 1 |
| 2 |
③f′(x)=3x2+1=
| 1 |
| 2 |
④f′(x)=ex=
| 1 |
| 2 |
故直线y=
| 1 |
| 2 |
故答案为:②④.

练习册系列答案
相关题目
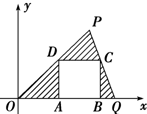 t∈R,且t∈(0,10),由t确定两个任意点P(t,t),Q(10-t,0).
t∈R,且t∈(0,10),由t确定两个任意点P(t,t),Q(10-t,0).