题目内容
8.P,Q为椭圆上的任意两点,延长PQ交焦点F所对应的准线于点R,求证:FR为∠PFQ的外角平分线.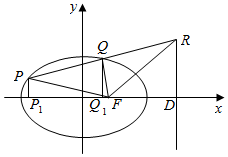
分析 可设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),右焦点F(c,0),右准线为l:x=$\frac{{a}^{2}}{c}$,过P,Q向准线分别作垂线PP1,QQ1交准线于P1,Q1,由椭圆的第二定义,结合平行线分线段成比例,以及外角平分线的判定定理,即可得证.
解答 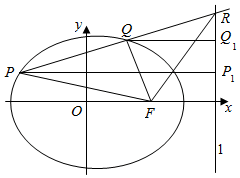 证明:可设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
证明:可设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
右焦点F(c,0),右准线为l:x=$\frac{{a}^{2}}{c}$,
过P,Q向准线分别作垂线PP1,QQ1交准线于P1,Q1,
由椭圆的第二定义,可得e=$\frac{PF}{P{P}_{1}}$=$\frac{QF}{Q{Q}_{1}}$,
即有$\frac{QF}{PF}$=$\frac{Q{Q}_{1}}{P{P}_{1}}$,
又QQ1∥PP1,可得
$\frac{Q{Q}_{1}}{P{P}_{1}}$=$\frac{QR}{PR}$,
即有$\frac{QF}{PF}$=$\frac{QR}{PR}$,
由外角平分线的判定定理,
可得FR为∠PFQ的外角平分线.
点评 本题考查椭圆的定义、方程和性质,考查定义法的运用,以及平行线分线段成比例,同时考查外角平分线的判定定理,属于中档题.

练习册系列答案
相关题目
19.已知三棱锥ABCD中,AB⊥CD,且AB与平面BCD成60°角.当$\frac{{S}_{△BCD}}{{S}_{△ACD}}$的值取到最大值时,二面角A-CD-B的大小为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
16.已知$\overrightarrow{a}$$⊥\overrightarrow{b}$,|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,且3$\overrightarrow{a}$$+2\overrightarrow{b}$与λ$\overrightarrow{a}$$-\overrightarrow{b}$垂直,则λ等于( )
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | ±$\frac{3}{2}$ | D. | 1 |
17.若θ是第二象限角,则( )
| A. | sin$\frac{θ}{2}$>0 | B. | tan$\frac{θ}{2}$>1 | C. | sin$\frac{θ}{2}$$>cos\frac{θ}{2}$ | D. | sin$\frac{θ}{2}$$<cos\frac{θ}{2}$ |
16.已知直线a,b,c和平面α,给出下列两个命题:
命题p:若a∥α,b∥α,则a∥b;
命题q:若a∥b,b∥c,则a∥c.
那么下列判断正确的是( )
命题p:若a∥α,b∥α,则a∥b;
命题q:若a∥b,b∥c,则a∥c.
那么下列判断正确的是( )
| A. | p为真命题 | B. | q为假命题 | C. | (¬p)∧q为真命题 | D. | (¬p)∨q为假命题 |