题目内容
△ABC中，内角A、B、C所对的边的长分别为a，b，c，且a2=b（b+c），则
= ．
| B |
| A |
考点：余弦定理
专题：三角函数的求值
分析：利用余弦定理列出关系式，将已知等式变形为a2=b2+bc代入，约分后再将b+c=
代入，利用正弦定理化简得到sinA=2sinBcosB=sin2B，进而得到A=2B，即可求出所求式子的值．
| a2 |
| b |
解答：
解：∵a2=b（b+c），即a2=b2+bc，b+c=
，
∴由正弦、余弦定理化简得：cosB=
=
=
=
=
=
，
则sinA=sin2B，即A=2B或A+2B=π，
∵a2=b2+c2-2bccosA，且a2=b（b+c）=b2+bc，
∴cosA=
=
=
＞0，即c＞b，
∴C＞B，
∵A+B+C=π，
∴A+2B＜π，
故A+2B=π不成立，舍去，
∴A=2B，
则
=
．
故答案为：
| a2 |
| b |
∴由正弦、余弦定理化简得：cosB=
| a2+c2-b2 |
| 2ac |
| c2+bc |
| 2ac |
| b+c |
| 2a |
| a2 |
| 2ab |
| a |
| 2b |
| sinA |
| 2sinB |
则sinA=sin2B，即A=2B或A+2B=π，
∵a2=b2+c2-2bccosA，且a2=b（b+c）=b2+bc，
∴cosA=
| b2+c2-a2 |
| 2bc |
| b2+c2-b2-bc |
| 2bc |
| c(c-b) |
| 2bc |
∴C＞B，
∵A+B+C=π，
∴A+2B＜π，
故A+2B=π不成立，舍去，
∴A=2B，
则
| B |
| A |
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：此题考查了正弦、余弦定理，熟练掌握定理是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
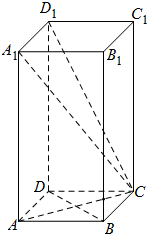已知正四棱柱ABCD-A1B1C1D1中，AB=2，AA1=4．