题目内容
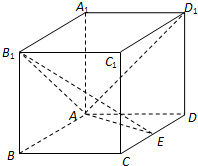
 如图,在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为CD中点.
如图,在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为CD中点.(1)求证:AD1⊥B1E;
(2)若AB=2,求平面AB1E把长方体ABCD-A1B1C1D1分成的两部分几何体的体积的比值.
考点:棱柱、棱锥、棱台的体积
专题:作图题,证明题,空间位置关系与距离
分析:(1)作辅助线B1C和A1D,证明AD1⊥面A1B1CD,从而证明AD1⊥B1E;(2)利用体积公式求解.
解答:
解:(1)连B1C和A1D
由长方体的性质可知CD⊥平面A1ADD1,从而CD⊥A1D
又AA1=AD=1,所以四边形AA1D1D是正方形
所以AD1⊥A1D
因为CD∩A1D=D,所以AD1⊥面A1B1CD
因为B1E?面A1B1CD,所以AD1⊥B1E
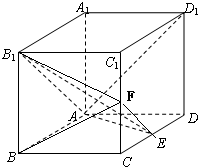
(2)取C1C中点F,连EF和B1F
易证EF||AB1,所以平面AB1E即为平面AEFB1,其把长方体ABCD-A1B1C1D1分成两部分.
连BF,则VF-ABCE=
SABCE•FC=
×
×(1+2)×1×
=
VF-ABB1=
SABB1•BC=
×
×2×1×1=
所以几何体CEF-ABB1的体积VCEF-ABB1=
+
=
而长方体的体积V=2×1×1=2
所以平面AB1E把长方体ABCD-A1B1C1D1分成的两部分
几何体的体积的比等于
=
由长方体的性质可知CD⊥平面A1ADD1,从而CD⊥A1D

又AA1=AD=1,所以四边形AA1D1D是正方形
所以AD1⊥A1D
因为CD∩A1D=D,所以AD1⊥面A1B1CD
因为B1E?面A1B1CD,所以AD1⊥B1E
(2)取C1C中点F,连EF和B1F
易证EF||AB1,所以平面AB1E即为平面AEFB1,其把长方体ABCD-A1B1C1D1分成两部分.
连BF,则VF-ABCE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
所以几何体CEF-ABB1的体积VCEF-ABB1=
| 1 |
| 4 |
| 1 |
| 3 |
| 7 |
| 12 |

而长方体的体积V=2×1×1=2
所以平面AB1E把长方体ABCD-A1B1C1D1分成的两部分
几何体的体积的比等于
| ||
2-
|
| 7 |
| 17 |
点评:考查了空间中线线垂直、线面垂直的证明与性质,及几何体的体积求法.属于中档题.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目