题目内容
设双曲线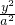
-
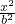=1（a＞0，b＞0）的渐近线与抛物线y=x2+1相切，则该双曲线的离心率等于________．
分析：把渐近线的方程与抛物线的方程联立消去y，利用判别式等于0求得a和b的关系，进而利用c=
求得a和c的关系，进而求得答案．解答：取一条渐近线方程y=
x，代入抛物线方程得x=x2+1∵渐近线与抛物线y=x2+1相切
∴△=
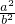-4=0，求得a=2b，∴c=
=
b∴e=
=
=，故答案为：
点评：本题主要考查了双曲线的简单性质．对于求得双曲线的离心率，关键是通过挖掘题设中的信息找到a和c的关系．
练习册系列答案
智慧小复习系列答案
相关题目
-
=1（a＞0，b＞0）的虚轴长为2，焦距为2
，则双曲线的渐近线方程为（ ）
-
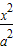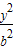=1（a＞0，b＞0）的离心率为
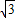，且它的一条准线与抛物线y2=4x的准线重合，则此双曲线的方程为（ ）
-
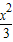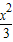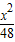=1
-
=1
-
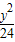=1
-
=1
=1（a＞0，b＞0）的右顶点为A，P为双曲线上的一个动点（不是顶点），从点A引双曲线的两条渐近线的平行线，与直线OP分别交于Q，R两点，其中O为坐标原点，则|OP|2与|OQ|•|OR|的大小关系为（ ）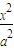
-
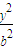=1（a＞0，b＞0）的右焦点为F，右准线l与两条渐近线交于P、Q两点，如果△PQF是直角三角形，则双曲线的离心率e= ．
-
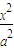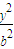=1（a＞0，b＞0）的渐近线与曲线y=x2+
相切，则该双曲线的离心率等于（ ）
