题目内容
4.如图,在正方体ABCD-A1B1C1D1,若E是AD的中点,则异面直线A1B与C1E所成角等于90°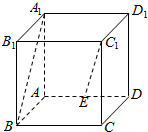
分析 以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,利用向量法能求出异面直线A1B与C1E所成角.
解答 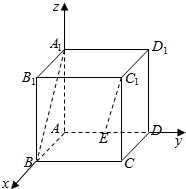 解:以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,
解:以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1的棱长为2,
则A1(0,0,2),B(2,0,0),C1(2,2,2),E(0,1,0),
$\overrightarrow{{{A}_{1}B}^{\;}}$=(2,0,-2),$\overrightarrow{{C}_{1}E}$=(-2,-1,-2),
设异面直线A1B与C1E所成角为θ,
则cosθ=$\frac{|\overrightarrow{{A}_{1}B}•\overrightarrow{{C}_{1}E}|}{|\overrightarrow{{A}_{1}B}|•|\overrightarrow{{C}_{1}E}|}$=$\frac{|-4+4|}{\sqrt{8}•\sqrt{9}}$=0,
∴θ=90°.
∴异面直线A1B与C1E所成角等于90°.
故答案为:90°.
点评 本题考查异面直线所成角的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
15.设全集U=R,集合A={x|y=lgx},B={-1,1},则下列结论正确的是( )
| A. | A∩B={-1} | B. | (∁RA)∪B=(-∞,0) | C. | A∪B=(0,+∞) | D. | (∁RA)∩B={-1} |
19.两圆${C_1}:{x^2}+{y^2}-1=0$和${C_2}:{x^2}+{y^2}-4x-5=0$的位置关系是( )
| A. | 相交 | B. | 外离 | C. | 外切 | D. | 内切 |
9.在△ABC中,a、b、c分别是角A、B、C的对边,若$sinBsinC-cosBcosC=\frac{1}{2}$.
(Ⅰ)求角A;
(Ⅱ)若$a=2,b+c=2\sqrt{3}$,求△ABC的面积.
(Ⅰ)求角A;
(Ⅱ)若$a=2,b+c=2\sqrt{3}$,求△ABC的面积.
14.把函数y=sin3x的图象向右平移$\frac{π}{4}$个长度单位,所得曲线的对应函数式( )
| A. | y=sin(3x-$\frac{3π}{4}$) | B. | y=sin(3x+$\frac{π}{4}$) | C. | y=sin(3x-$\frac{π}{4}$) | D. | y=sin(3x+$\frac{3π}{4}$) |