题目内容
8.m,n,l是直线,α,β是两个不同的平面,下面说法正确的是( )| A. | 若m∥α,m∥β,则α∥β | |
| B. | 若m?α,n?α,l⊥m,l⊥n,则l⊥α | |
| C. | 若m?α,n?α,m,n是异面直线,则n与α相交 | |
| D. | 若m⊥α,m?β,则α⊥β |
分析 可以结合具体图象,利用反例法判断,过程如下解题.
解答 解:若m∥α,m∥β,则α,β有肯能相交,故A错误;
B中要求m,n是相交直线,故B错误;
C中n与α也可以平行,故C错误;
D为判断两平面垂直的判定定理,正确
故选:D.
点评 考查了空间图形中线面的位置关系,属于基础题型,应熟练掌握.

练习册系列答案
相关题目
3.函数f(x)=x2-bx+c,满足f(x)=f(2-x)且f(0)=3,则f(b-x)与f(c-x)的关系是( )
| A. | f(b-x)≥f(c-x) | B. | f(b-x)≤f(c-x) | C. | f(b-x)>f(c-x) | D. | 不能确定 |
16.将二次函数y=x2的图象向左平移2个单位,再向下平移3个单位,得到的函数的解析式为( )
| A. | y=x2+4x+7 | B. | y=x2+4x+1 | C. | y=x2-4x+7 | D. | y=x2-4x-7 |
3.已知三个平面两两垂直,给出命题:①它们的交线一定交于一点; ②它们的交线一定两两垂直; ③其中任意两个平面的交线一定与第三个平面垂直;④它们将空间分成8部分; 其中正确的命题一共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.已知某等差数列共有20项,其奇数项之和为15,偶数项之和为35,则其公差为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
20.数列{an}满足an+1+(-1)nan=2n-1,则{an}的前60项和为( )
| A. | 1830 | B. | 1845 | C. | 3660 | D. | 3690 |
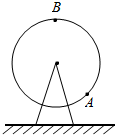 乐场有一个按逆时针方向旋转的大风车,如图所示.已知某人从点A处上风车,离地面的高度h(米)与它登上大风车后运行的时间t(分钟)满足函数关系h=12.5+10cos($\frac{2π}{15}$t-$\frac{2π}{3}$),且5分钟后到达顶点B.
乐场有一个按逆时针方向旋转的大风车,如图所示.已知某人从点A处上风车,离地面的高度h(米)与它登上大风车后运行的时间t(分钟)满足函数关系h=12.5+10cos($\frac{2π}{15}$t-$\frac{2π}{3}$),且5分钟后到达顶点B.