题目内容

若loga＜1,求实数a的取值范围.

解法一:由loga＜1得＜1,

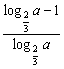即＞0,

即loga＞1=log或loga＜0=log1.

而y=logx在(0,+∞)上单调递减,

∴0＜a＜或a＞1.

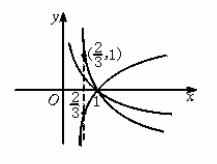
解法二:在上图中,经过点(,1)的对数函数为y=logx,而由底数与对数函数图象的规律可知,要使函数f(x)=logax满足f()=loga＜1,则必有0＜a＜或a＞1.

练习册系列答案
相关题目
已知全集U=R，集合A={x|
12
＜2x-4＜4}，B={x|x2-11x+18＜0}．
（Ⅰ）分别求?R（A∪B），（?RA）∩B；
（Ⅱ）已知C={x|a＜x＜a+1}，若C⊆B，求实数a的取值范围．
设全集是实数集R，A={x|x2-4x+3≤0}，B={x|x2-a＜0}．
（1）当a=4时，求A∩B和A∪B；
（2）若B⊆?RA，求实数a的取值范围．
已知直线l1：ax+3y+1=0，l2：x+（a-2）y+a=0．
（1）若l1⊥l2，求实数a的值；
（2）当l1∥l2时，求直线l1与l2之间的距离．
已知集合P={x|
1
2
≤x≤3}，集合Q是函数f（x）=log2（ax2-2x+2）的定义域．
（1）若P∩Q=[
1
2
，
2
3
)，P∪Q=(-2，3]，求实数a的值；
（2）若P∩Q=∅，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网