题目内容
8. 如图,在正方体..中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的正(主)视图与侧(左)视图的面积的比值为1.
如图,在正方体..中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的正(主)视图与侧(左)视图的面积的比值为1.
分析 由题意确定P在主视图中的射影到AB在平面CDD1C1上的射影的距离,P的射影在左视图中到AC在平面BCC1B1三度射影的距离,即可求出主视图与左视图的面积的比值.
解答 解:由题意可知,P在主视图中的射影是在C1D1上,
AB在主视图中,在平面CDD1C1上的射影是CD,P的射影到CD的距离是正方体的棱长;
P在左视图中,的射影是在B1C1上,
在左视图中AC在平面BCC1B1三度射影是BC,P的射影到BC的距离是正方体的棱长,
所以三棱锥P-ABC的主视图与左视图的面积的比值为:$\frac{\frac{1}{2}C{D}^{2}}{\frac{1}{2}C{D}^{2}}$=1.
故答案为1.
点评 本题考查三视图与直观图形的关系,正确处理正射影与射影图形是解题的关键,考查空间想象能力,计算能力.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
20.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(-$\frac{π}{6}$)的值为( )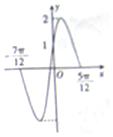

| A. | -1 | B. | 1 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
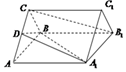 如图,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是$\sqrt{3}$,D是AC的中点.
如图,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是$\sqrt{3}$,D是AC的中点.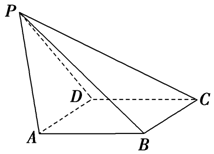 如图,已知四棱锥P-ABCD,侧面PAD是正三角形,底面ABCD是菱形,∠BAD=60°,设平面PAD∩平面PBC=l.
如图,已知四棱锥P-ABCD,侧面PAD是正三角形,底面ABCD是菱形,∠BAD=60°,设平面PAD∩平面PBC=l. 如图,等腰梯形ABCD中,AB∥CD,AD⊥BD,矩形ABEF所在的平面和平面ABCD相互垂直.
如图,等腰梯形ABCD中,AB∥CD,AD⊥BD,矩形ABEF所在的平面和平面ABCD相互垂直.