题目内容
正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( )
A. B.16π C.9π D.
B.16π C.9π D.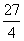
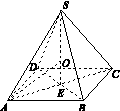
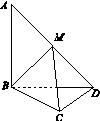
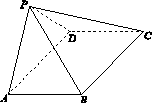
A [解析] 如图所示,因为正四棱锥的底面边长为2,所以AE= AC=
AC= .设球心为O,球的半径为R,则OE=4-R,OA=R,又知△AOE为直角三角形,根据勾股定理可得,OA2=OE2+AE2,即R2=(4-R)2+2,解得R=
.设球心为O,球的半径为R,则OE=4-R,OA=R,又知△AOE为直角三角形,根据勾股定理可得,OA2=OE2+AE2,即R2=(4-R)2+2,解得R= ,所以球的表面积S=4πR2=4π×
,所以球的表面积S=4πR2=4π×
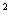 =
= .
.

练习册系列答案
相关题目
为质检某产品的质量,现抽取5件,测量产品中微量元素x,y的含量(单位:毫克),测量数据如下:
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 70 | 81 |
如果产品中的微量元素x,y满足x≥175且y≥75时,该产品为优等品.现从上述5件产品中,随机抽取2件,则抽取的2件产品中优等品数X的分布列为________.
 的概率是________.
的概率是________.


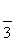 ,M为BC上一点,且BM=
,M为BC上一点,且BM=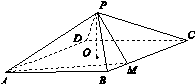
 .
.