题目内容
四面体ABCD及其三视图如图14所示,过棱AB的中点E作平行于AD,BC的平面分别交四面体的棱BD,DC,CA于点F,G,H.
(1)证明:四边形EFGH是矩形;
(2)求直线AB与平面EFGH夹角θ的正弦值.
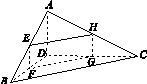
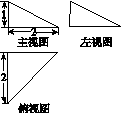
图14
解:(1)证明:由该四面体的三视图可知,
BD⊥DC,BD⊥AD,AD⊥DC,
BD=DC=2,AD=1.
由题设,BC∥平面EFGH,
平面EFGH∩平面BDC=FG,
平面EFGH∩平面ABC=EH,
∴BC∥FG,BC∥EH,∴FG∥EH.
同理EF∥AD,HG∥AD,∴EF∥HG.
∴四边形EFGH是平行四边形.
又∵AD⊥DC,AD⊥BD,∴AD⊥平面BDC,
∴AD⊥BC,∴EF⊥FG,
∴四边形EFGH是矩形.

(2)方法一:如图,以D为坐标原点建立空间直角坐标系,则D(0,0,0),A(0,0,1),B(2,0,0),C(0,2,0),
DA=(0,0,1),BC=(-2,2,0),
BA=(-2,0,1).
设平面EFGH的法向量n=(x,y,z),
∵EF∥AD,FG∥BC,
∴n·DA=0,n·BC=0,
得
方法二:如图,以D为坐标原点建立空间直角坐标系,
则D(0,0,0),A(0,0,1),B(2,0,0),C(0,2,0),
∵E是AB的中点,∴F,G分别为BD,DC的中点,得 ,F(1,0,0),G(0,1,0).
,F(1,0,0),G(0,1,0).


计划在某水库建一座至多安装3台发电机的水电站.过去50年的水文资料显示,水库年入流量X(年入流量:一年内上游来水与库区降水之和,单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多有1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量X限制,并有如下关系:
| 年入流量X | 40<X<80 | 80≤X≤120 | X>120 |
| 发电机最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5 000万元;若某台发电机未运行,则该台年亏损800万元.欲使水电站年总利润的均值达到最大,应安装发电机多少台.



 B.
B.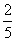 C.
C.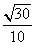 D.
D.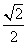
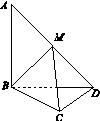
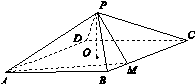
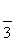 ,M为BC上一点,且BM=
,M为BC上一点,且BM= ,MP⊥AP.
,MP⊥AP.