题目内容
14．曲线y=-5ex+4在点（0，-1）处的切线方程为y=-5x-1．分析 求出函数的导数，求得切线的斜率，运用斜截式方程即可得到所求切线的方程．
解答 解：y=-5ex+4的导数为y′=-5ex，
即有在点（0，-1）处的切线的斜率为k=-5，
则点（0，-1）处的切线方程为y=-5x-1．
故答案为：y=-5x-1．
点评 本题考查导数的运用：求切线的方程，考查直线方程的运用，属于基础题．
练习册系列答案
相关题目
9．等差数列{an}的前n项和为Sn，且a3=5，则S5=（ ）
| A． | 3 | B． | 5 | C． | 9 | D． | 25 |
6．设f（x）=ax2+bx+c（a＞0）满足f（1+x）=f（1-x），则f（2x）与f（3x）的大小关系为（ ）
| A． | f （3x）≥f （2x） | B． | f （3x）≤f （2x） | C． | f （3x）＜f （2x） | D． | 不确定 |
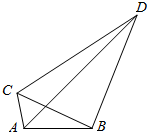如图，△ABC与△CBD都是直角三角形，∠BAC=∠DBC=90°，∠ABC=∠BDC=30°，若$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$，求x，y的值．