题目内容
对定义在![]() 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数![]() 称为
称为![]() 函数.① 对任意的
函数.① 对任意的![]() ,总有
,总有![]() ;
;
② 当![]() 时,总有
时,总有![]() 成立.
成立.
已知函数![]() 与
与![]() 是定义在
是定义在![]() 上的函数.
上的函数.
(1)试问函数![]() 是否为
是否为![]() 函数?并说明理由;
函数?并说明理由;
(2)若函数![]() 是
是![]() 函数,求实数
函数,求实数![]() 的值;
的值;
(3)在(2)的条件下,若方程![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
解:(1)当![]() 时,总有
时,总有![]() 满足①……………………………1分
满足①……………………………1分
当![]() 时,
时,
![]() 满足②………3分
满足②………3分
所以函数![]() 为
为![]() 函数;………………………………………………………4分
函数;………………………………………………………4分
(2)因为函数![]() 是
是![]() 函数,根据①有
函数,根据①有![]() ,……………6分
,……………6分
根据②有![]() ,
,
![]()
![]() …………………………………………………7分
…………………………………………………7分
因为![]() ,
,
所以![]() ,
,![]() ,其中
,其中![]() 和
和![]() 不能同时取到
不能同时取到![]() ,
,
于是![]() ,……………………8分
,……………………8分
所以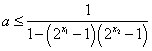 ,即
,即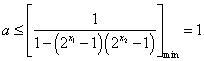 ,……………9分
,……………9分
于是![]() …………………………………………………………………………10分
…………………………………………………………………………10分
另解:因为函数![]() 是
是![]() 函数,根据①有
函数,根据①有![]() ,…………6分
,…………6分
根据②有![]()
![]() ………………………………8分
………………………………8分
取![]() 得
得![]() …………………………………………………………9分
…………………………………………………………9分
于是![]() …………………………………………………………………………10分
…………………………………………………………………………10分
(3)根据(2)知![]() ,原方程可以化为
,原方程可以化为![]() ,…………………11分
,…………………11分
由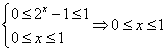 ,……………………………………………………12分
,……………………………………………………12分
令![]() ,则
,则![]() ,……………………………13分
,……………………………13分
因此,当![]() 时,方程有解
时,方程有解

练习册系列答案
相关题目
 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为 函数。
函数。 ,总有
,总有 ;
; 时,总有
时,总有 成立。
成立。 与
与 是定义在
是定义在 是否为
是否为 函数?并说明理由;
函数?并说明理由; 是
是 的值;
的值;
 解的个数情况。
解的个数情况。 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为 函数.
函数. ,总有
,总有 ;
; 时,总有
时,总有 成立.
成立. 与
与 是定义在
是定义在 是否为
是否为 函数?并说明理由;
函数?并说明理由; 是
是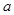 的值;
的值; ,使方程
,使方程 恰有两解?若存在,求出实数
恰有两解?若存在,求出实数