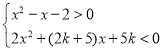题目内容
【题目】已知幂函数![]() 满足
满足![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若函数![]() ,是否存在实数
,是否存在实数![]() 使得
使得![]() 的最小值为0?若存在,求出
的最小值为0?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)若函数![]() ,是否存在实数
,是否存在实数![]() ,使函数
,使函数![]() 在
在![]() 上的值域为
上的值域为![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【答案】(1)![]() ;(2)存在
;(2)存在![]() 使得
使得![]() 的最小值为0;(3)
的最小值为0;(3)![]() .
.
【解析】试题分析:(1)由![]() 为幂函数可得
为幂函数可得![]() ,解得
,解得![]() 或
或![]() ,经验证
,经验证![]() 。(2)令
。(2)令![]() ,则
,则![]() ,设
,设![]() ,则将问题转化为函数
,则将问题转化为函数![]() 在
在![]() 上的最小值是否为0的问题。根据对称轴
上的最小值是否为0的问题。根据对称轴![]() 与区间
与区间![]() 的关系求解,可得
的关系求解,可得![]() 满足题意。(3)由题意得
满足题意。(3)由题意得![]() ,且
,且![]() 在定义域内为单调递减函数,若存在实数a,b满足题意,则可得
在定义域内为单调递减函数,若存在实数a,b满足题意,则可得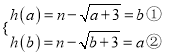 ,由②-①消去n得
,由②-①消去n得![]() ,从而
,从而![]() ,将③代入②得
,将③代入②得![]() ,再令
,再令![]() ,由
,由![]() 得
得![]() ,所以将问题转化为求
,所以将问题转化为求![]() 在
在
![]() 上的取值范围,根据二次函数的知识可得
上的取值范围,根据二次函数的知识可得![]() 。
。
试题解析:
(1)∵![]() 是幂函数,
是幂函数,
∴![]() ,
,
解得![]() 或
或![]() ,
,
当![]() 时,
时, ![]() ,不满足
,不满足![]() ,
,
当![]() 时,
时, ![]() ,满足
,满足![]() ,
,
∴![]()
∴![]() 。
。
(2)令![]() ,则
,则![]() ,
,
设![]() ,
,
①当![]() ,即
,即![]() 时,由题意得
时,由题意得
![]() ,
,
解得![]() ;
;
②当![]() ,即
,即![]() 时,由题意得
时,由题意得
![]() ,
,
解得![]() (舍去);
(舍去);
③当![]() ,即
,即![]() 时,由题意得
时,由题意得
![]() ,
,
解得![]() (舍去)
(舍去)
综上存在![]() 使得
使得![]() 的最小值为0。
的最小值为0。
(3)由题意得![]() ,
,
∴![]() 在定义域内为单调递减函数;
在定义域内为单调递减函数;
若存在实数![]() ,使函数
,使函数![]() 在
在![]() 上的值域为
上的值域为![]() ,
,
则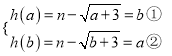 ,
,
由②-①,得
![]() ,
,
∴![]() ,
,
将③代入②得,
![]() ,
,
令![]() ,
,
∵![]() ,
,
∴![]() ,
,
又![]() ,故在区间
,故在区间![]() 上单调递减,
上单调递减,
∴![]() 。
。
∴存在实数![]() ,使函数
,使函数![]() 在
在![]() 上的值域为
上的值域为![]() 且实数
且实数![]() 的取值范围为
的取值范围为
![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某种植基地将编号分别为1,2,3,4,5,6的六个不同品种的马铃薯种在如图所示的
A | B | C | D | E | F |
这六块实验田上进行对比试验,要求这六块实验田分别种植不同品种的马铃薯,若种植时要求编号1,3,5的三个品种的马铃薯中至少有两个相邻,且2号品种的马铃薯不能种植在A、F这两块实验田上,则不同的种植方法有 ( )
A. 360种 B. 432种 C. 456种 D. 480种
【题目】汽车急刹车的停车距离与诸多因素有关,其中最为关键的两个因素是驾驶员的反应时间和汽车行驶的速度.设d表示停车距离,![]() 表示反应距离,
表示反应距离,![]() 表示制动距离,则
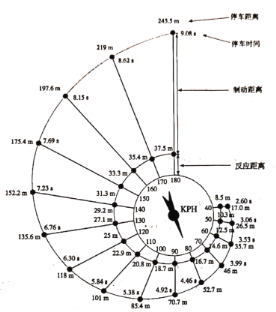
表示制动距离,则![]() .下图是根据美国公路局公布的试验数据制作的停车距离示意图,对应的汽车行驶的速度与停车距离的表格如下图所示
.下图是根据美国公路局公布的试验数据制作的停车距离示意图,对应的汽车行驶的速度与停车距离的表格如下图所示
序号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据表格中的数据,建立停车距离与汽车速度的函数模型.可选择模型一:![]() 或模型二:
或模型二:![]() (其中v为汽车速度,a,b
(其中v为汽车速度,a,b
(2)通过计算![]() 时的停车距离,分析选择哪一个函数模型的拟合效果更好.
时的停车距离,分析选择哪一个函数模型的拟合效果更好.
(参考数据:![]() ;
;![]() ;
;![]() .)
.)