题目内容
函数f(x)=x2-ax+b,a,b∈R.若f(x)在区间(-∞,1)上单调递减,则a的取值范围 .
考点:二次函数的性质
专题:函数的性质及应用
分析:根据题意要满足f(x)在区间(-∞,1)上单调递减,要求函数图象的对称轴必须在直线x=1的右侧或重合,求得a的范围.
解答:
解:依题意可知函数的图象为抛物线,开口向上,对称轴方程为x=
,
要使f(x)在区间(-∞,1)上单调递减,需
≥1,即a≥2,
故答案为:a≥2.
| a |
| 2 |
要使f(x)在区间(-∞,1)上单调递减,需
| a |
| 2 |
故答案为:a≥2.
点评:本题主要考查了二次函数的性质.结合二次函数的图象,充分利用好函数对称轴的位置,求得a的范围.

练习册系列答案
相关题目
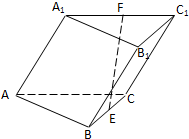 如图,斜三棱柱ABC-A1B1C1的侧棱长为
如图,斜三棱柱ABC-A1B1C1的侧棱长为