题目内容
已知函数f(x)=cos(2x- )+sin2x-cos2x.
)+sin2x-cos2x.
(1)求函数f(x)的最小正周期及图象的对称轴方程;
(2)设函数g(x)=[f(x)]2+f(x),求g(x)的值域.
解:(1)f(x)= cos2x+
cos2x+ sin2x-cos2x
sin2x-cos2x
= sin2x-
sin2x- cos2x=sin(2x-
cos2x=sin(2x- ).
).
∴最小正周期T= =π.
=π.
由2x- =kπ+
=kπ+ ,k∈Z,得x=
,k∈Z,得x= +
+ ,k∈Z.
,k∈Z.
∴函数图象的对称轴方程为x= +
+ ,k∈Z.
,k∈Z.
(2)g(x)=[f(x)]2+f(x)
=sin2(2x- )+sin(2x-
)+sin(2x- )
)
=[sin(2x- )+
)+ ]2-
]2-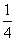 .
.
当sin(2x- )=-
)=- 时,g(x)取得最小值-
时,g(x)取得最小值-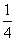 ,
,
当sin(2x- )=1时,g(x)取得最大值2.
)=1时,g(x)取得最大值2.
∴g(x)的值域为[-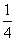 ,2].
,2].

练习册系列答案
相关题目
 ,
, (
( 为常数),函数
为常数),函数 图象上横坐标为
图象上横坐标为 的点处的切线
的点处的切线 ,与函数
,与函数 的图象相切.
的图象相切. ,求函数
,求函数 的极值.
的极值. (
( )的图象经过
)的图象经过
 两点,则
两点,则 的最小值为____________.
的最小值为____________.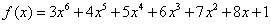 用秦九韶算法计算多
用秦九韶算法计算多  的图像关于点
的图像关于点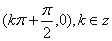 对称;
对称; 是最小正周期为
是最小正周期为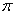 的周期函数;
的周期函数;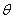 为第二象限的角,则
为第二象限的角,则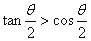 ,且
,且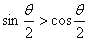 ;
;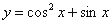 的最小值为-1;
的最小值为-1; 的一条斜线有一个平面与平面
的一条斜线有一个平面与平面 ”是“
”是“ ”的必要条件;
”的必要条件; ”的否定是“
”的否定是“ ”,“
”,“ ”,若
”,若 是
是 的充分不必要条件,则
的充分不必要条件,则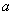 的取值范围是 .
的取值范围是 . ,如果
,如果 是
是 的充分不必要条件,则实数
的充分不必要条件,则实数 的取值范围是( )
的取值范围是( )  B.
B. C.
C. D.
D.
 与函数
与函数 的图象恰有三个不同的公共点,则实数
的图象恰有三个不同的公共点,则实数 的取值范围是 .
的取值范围是 .