题目内容
已知函数 ,
, (
( 为常数),函数
为常数),函数 图象上横坐标为
图象上横坐标为 的点处的切线
的点处的切线 ,与函数
,与函数 的图象相切.
的图象相切.
(Ⅰ)求直线 的方程及
的方程及 的值;
的值;
(Ⅱ)若 ,求函数
,求函数 的极值.
的极值.
解:(Ⅰ)由题意得: 与函数y=
与函数y=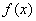 图象的切点为(1,
图象的切点为(1,
∵切点(1, 在
在 图象上
图象上
∴切点为(1,0) ………………………………………………………………………2分
又∵

∴直线 的斜率为:
的斜率为: …………………………………………………………4分
…………………………………………………………4分
∴直线 的
的 ……………………………………………………………………5分
……………………………………………………………………5分
∵直线 与函数y=
与函数y= 的图象相切
的图象相切
∴方程组
 只有一个解,即方程
只有一个解,即方程
∴△=0,解得 ……………7分
……………7分
(Ⅱ)由(I)得
∴ ,且
,且 的定义域为
的定义域为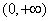 ……………9分
……………9分
又∵
令 ,得
,得 ,或
,或 (舍去)…………………11分
(舍去)…………………11分
当 变化时,
变化时, ,
, 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
| 单调递增 |
| 单调递减 |
…………………13分
∴当 时,函数
时,函数 有极大值,极大值为
有极大值,极大值为 ,函数
,函数 没有极小值。………14分
没有极小值。………14分

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
某大学准备在开学时举行一次大学一年级学生座谈会,拟邀请 名来自本校机械工程学院、海洋学院、医学院、经济学院的学生参加,各学院邀请的学生数如下表所示:
名来自本校机械工程学院、海洋学院、医学院、经济学院的学生参加,各学院邀请的学生数如下表所示:
| 学院 | 机械工程学院 | 海洋学院 | 医学院 | 经济学院 |
| 人数 |
|
|
|
|
(Ⅰ)从这 名学生中随机选出
名学生中随机选出 名学生发言,求这
名学生发言,求这 名学生中任意两个均不属于同一学院的概率;
名学生中任意两个均不属于同一学院的概率;
(Ⅱ)从这 名学生中随机选出
名学生中随机选出 名学生发言,设来自医学院的学生数为
名学生发言,设来自医学院的学生数为 ,求随机变量
,求随机变量 的概率分布列和数学期望.
的概率分布列和数学期望.


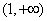



 R
R ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 .
. 的解析式;
的解析式; 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,给出以下几个结论:①f (x)>0的解集是{x|0<x<1};②
,给出以下几个结论:①f (x)>0的解集是{x|0<x<1};② 既有极小值,又有极大值;③f (x)没有最小值,也没有最大值;④f (x)有最大值,没有最小值.其中判断正确的是______.
既有极小值,又有极大值;③f (x)没有最小值,也没有最大值;④f (x)有最大值,没有最小值.其中判断正确的是______.  在点
在点 处的切线与坐标轴所围三角形的面积为( )
处的切线与坐标轴所围三角形的面积为( ) B.
B. C.
C. D.
D.
 ,给出以下几个结论:①
,给出以下几个结论:① 的解集是{x|0<x<1};②
的解集是{x|0<x<1};② 则
则 为 ( )
为 ( )  B.
B. C.
C. D.
D.


 )+sin2x-cos2x.
)+sin2x-cos2x.