题目内容
已知函数f(x)=x2+2x+a和函数g(x)=2x+ ,对任意x1∈[-1,+∞),总存在x2∈R使g(x1)=f(x2)成立,则实数a的取值范围是________.
,对任意x1∈[-1,+∞),总存在x2∈R使g(x1)=f(x2)成立,则实数a的取值范围是________.
(-∞,-1]解析 因为f(x)=x2+2x+a=(x+1)2+a-1,
所以f(x)∈[a-1,+∞).
因为g(x)=2x+ 在[-1,+∞)上单调递增,
在[-1,+∞)上单调递增,
所以g(x)∈[-2,+∞).由题意得a-1≤-2,
所以a≤-1,故实数a的取值范围是(-∞,-1].

练习册系列答案
相关题目
 恰好被面积最小的圆
恰好被面积最小的圆
 及其内部所覆盖.(1)试求圆
及其内部所覆盖.(1)试求圆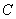 的方程;(2)若斜率为
的方程;(2)若斜率为 的直线
的直线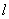 与圆
与圆 ,满足
,满足 ,求直线
,求直线 则f
则f =( )
=( )

 的定义域为R,则a的取值范围是________.
的定义域为R,则a的取值范围是________.