题目内容
14.在△ABC中,内角A,B,C的对边分别为a,b,c,且a>b,a>c.△ABC的外接圆半径为1,$a=\sqrt{3}$,若边BC上一点D满足BD=2DC,且∠BAD=90°,则△ABC的面积为$\frac{\sqrt{3}}{4}$.分析 由已知及正弦定理可求sinA=$\frac{\sqrt{3}}{2}$,进而可求A,∠CAD,BD,CD,由正弦定理可得b=$\frac{2}{\sqrt{3}}$sin∠2=$\frac{2}{\sqrt{3}}$sin∠1=$\frac{2}{\sqrt{3}}$$\frac{\frac{c}{2}}{\sqrt{3}}$=c,可求sinB=$\frac{1}{2}$,c=1,即可利用三角形面积公式计算得解.
解答 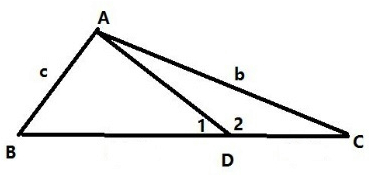 解:∵△ABC的外接圆半径R为1,$a=\sqrt{3}$,
解:∵△ABC的外接圆半径R为1,$a=\sqrt{3}$,
∴由正弦定理$\frac{a}{sinA}=2R$,
可得:sinA=$\frac{\sqrt{3}}{2}$,
∵边BC上一点D满足BD=2DC,
且∠BAD=90°,
∴A=120°,∠CAD=30°,
BD=$\frac{2}{3}$a=$\frac{2\sqrt{3}}{3}$,CD=$\frac{1}{3}$a=$\frac{\sqrt{3}}{3}$,
∴如图,由正弦定理可得:$\frac{b}{sin2}=\frac{\frac{1}{\sqrt{3}}}{\frac{1}{2}}$,可得:b=$\frac{2}{\sqrt{3}}$sin∠2=$\frac{2}{\sqrt{3}}$sin∠1=$\frac{2}{\sqrt{3}}$$\frac{\frac{c}{2}}{\sqrt{3}}$=c,
∴△BAC是等腰三角形,底角是30°,
∴sinB=$\frac{1}{2}$,可得:c=1,
∴S△ABC=$\frac{1}{2}×1×1×sin120°$=$\frac{\sqrt{3}}{4}$.
故答案为:$\frac{\sqrt{3}}{4}$.
点评 本题主要考查了正弦定理,三角形面积公式在解三角形中的应用,考查了数形结合思想,属于中档题.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案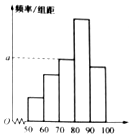 某教师为了分析所任教班级某将考试的成绩,将全班同学的成绩做出了频数与频率的统计表和频率分布直方图.
某教师为了分析所任教班级某将考试的成绩,将全班同学的成绩做出了频数与频率的统计表和频率分布直方图.| 分组 | 频数 | 频率 |
| [50,60) | 3 | 0.06 |
| [60,70) | m | 0.10 |
| [70,80) | 13 | n |
| [80,90) | p | q |
| [90,100] | 9 | 0.18 |
| 总计 | t | 1 |
(2)该教师从这次考试成绩低于70分的学生中随机抽取3人进行面批,设X表示所抽取学生中成绩低于60分的人数,求随机变量X的分布列和数学期望.