题目内容
已知椭圆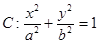 的短轴长等于焦距,椭圆C上的点到右焦点
的短轴长等于焦距,椭圆C上的点到右焦点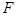 的最短距离为
的最短距离为 .(Ⅰ)求椭圆C的方程;(Ⅱ)过点
.(Ⅰ)求椭圆C的方程;(Ⅱ)过点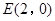 且斜率为
且斜率为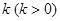 的直线
的直线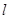 与
与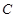 交于
交于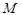 、
、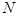 两点,
两点,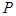 是点
是点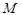 关于
关于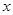 轴的对称点,证明:
轴的对称点,证明: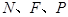 三点共线.
三点共线.
【答案】
(1) ;(2)见解析.
;(2)见解析.
【解析】本试题主要是考查了椭圆的方程和性质的运用,以及直线与椭圆的位置关系的运用。
(1)利用椭圆的几何性质得到a,b,c的关系式,从而解得
(2)联立直线与椭圆的方程,结合韦达定理和向量的关系式得到证明。
解:(I)由题可知: …………2分
…………2分
解得 ,
,
 椭圆C的方程为
椭圆C的方程为 …………………………4分
…………………………4分
(II)设直线 :
: ,
, ,
, ,
, ,
, ,
,
由 得
得 .…………6分
.…………6分
所以 ,
, . ……………………8分
. ……………………8分
而
 ,
, ,…………10分
,…………10分





∴ 三点共线
三点共线

练习册系列答案
相关题目
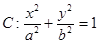 的短轴长等于焦距,椭圆C上的点到右焦点
的短轴长等于焦距,椭圆C上的点到右焦点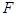 的最短距离为
的最短距离为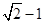 .
. 且斜率为
且斜率为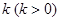 的直线
的直线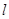 与
与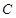 交于
交于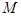 、
、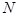 两点,
两点,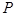 是点
是点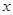 轴的对称点,证明:
轴的对称点,证明: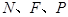 三点共线.
三点共线. ,则此椭圆的标准方程是 .
,则此椭圆的标准方程是 .