题目内容
在 中,角
中,角 所对的边分别为
所对的边分别为 ,且满足
,且满足 .
.
(1) 求角 的大小;
的大小;
(2) 当 取得最大值时,请判断
取得最大值时,请判断 的形状.
的形状.
(1) (2)等边三角形
(2)等边三角形
解析试题分析:(1)根据已知条件 ,可利用正弦定理变形解决;
,可利用正弦定理变形解决;
(2) 中有两个角都是未知的,所以得利用第(1)的结论换掉其中一个角,比如
中有两个角都是未知的,所以得利用第(1)的结论换掉其中一个角,比如 ,接下来
,接下来 中只含有角
中只含有角 ,利用余弦差角公式以及辅助角公式可化简该式,从而根据结果分析出三角形的形状.
,利用余弦差角公式以及辅助角公式可化简该式,从而根据结果分析出三角形的形状.
(1)由 结合正弦定理变形得:
结合正弦定理变形得:
从而 ,
, ,
,
∵ ,∴
,∴ ;
;
(2)由(1)知
则




∵ , ∴
, ∴
当 时,
时, 取得最大值1, 此时
取得最大值1, 此时 ,
, .
.
故此时 为等边三角形
为等边三角形
考点:正弦定理;换角思想;余弦差角公式,辅助角公式.

练习册系列答案
相关题目

 、
、 、
、 、
、 ,欲测量
,欲测量 米,如图,同时也能测量出
米,如图,同时也能测量出 ,
, ,
,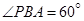 ,
, ,则
,则
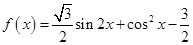 .
.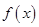 的最小正周期及在区间
的最小正周期及在区间 的最大值;
的最大值; 中,
中, 、
、 、
、 所对的边分别是
所对的边分别是 、
、 、
、 ,
, ,
, ,求
,求 周长
周长 的最大值.
的最大值. .
. ,且
,且 ,求
,求 的值;
的值; ,且△ABC的面积为
,且△ABC的面积为 ,求sinA+sinB的值.
,求sinA+sinB的值. 中,角
中,角 所对的边分别为
所对的边分别为 ,点
,点 在直线
在直线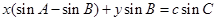 上.
上.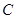 的值;
的值; ,且
,且 ,求
,求 .
. ,
, 

 .
. 的单调增区间;
的单调增区间; 中,
中,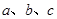 分别是角
分别是角 的对边,且
的对边,且 ,求
,求