题目内容
在△ABC中,AB=3,AC边上的中线BD= ,
, 
(1)求AC的长;
(2)求sin(2A-B)的值.
(1) AC=2;(2) sin(2A-B)=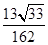
解析试题分析:(1)由已知条件可得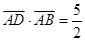 ,又
,又 ,进行向量运算可得
,进行向量运算可得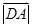 ,则求得AC;(2)先由向量的数量积求得
,则求得AC;(2)先由向量的数量积求得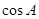 ,可得
,可得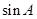 ,余弦定理求得BC,再正弦定理求得
,余弦定理求得BC,再正弦定理求得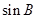 ,可得
,可得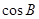 ,sin(2A-B)展开代入可得.
,sin(2A-B)展开代入可得.
解:(1) 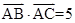 ,AB=3,AC=2AD, ∴
,AB=3,AC=2AD, ∴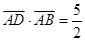 ,
,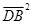 =
=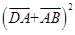 =
=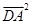 +
+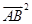 +2
+2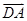 ·
·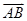 =
=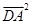 +9-
+9-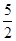 ×2=
×2=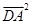 +4=5,
+4=5,
∴AD=|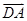 |=1,AC=2. 6分
|=1,AC=2. 6分
(2)由(1)得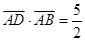 ,
,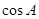 =
=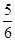 ,∴
,∴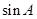 =
=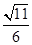 ,
,
在△ABC中,BC2=AB2+AC2-2AB·AC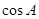 , ∴BC=
, ∴BC=
在△ABC中, 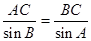 ,
,
∴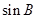 =
=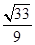 ,∴
,∴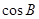 =
=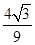 ,
,
sin(2A-B)=sin2A·cosB-cos2A·sinB=2sinA·cosA·cosB-(1-2sin2A)·sinB
=2×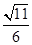 ×
×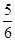 ×
×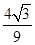 -
-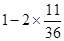 ×
×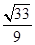 =
=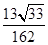 . 13分
. 13分
考点:向量的数量积,正弦定理,余弦定理.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 中,已知
中,已知 ,
, 且
且 .
. 和
和 的值;
的值; ,求边
,求边 的长.
的长. 是边长为1的正三角形,
是边长为1的正三角形, 分别是边
分别是边 上的点,
上的点, 过
过 ,设
,设 .
. 时,求
时,求 的长;
的长; 的面积为
的面积为 ,试将
,试将 的函数;
的函数; 的最大值和最小值。
的最大值和最小值。
 中,角
中,角 所对的边分别为
所对的边分别为 ,且满足
,且满足 .
. 的大小;
的大小; 取得最大值时,请判断
取得最大值时,请判断 ,
,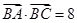 .
.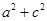 的值;
的值; 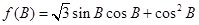 的值域.
的值域. ,设函数
,设函数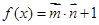 .
. 的单调递增区间;
的单调递增区间;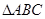 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且满足
,且满足 ,
, ,求
,求 的值.
的值. 中,
中, ,点
,点 是边
是边 上的动点,动点
上的动点,动点 满足
满足 (点
(点 按逆时针方向排列).
按逆时针方向排列).
 ,求
,求 的长;
的长; 面积的最大值.
面积的最大值. 中,角
中,角 、
、 、
、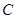 所对的边分别为
所对的边分别为 、
、 、
、 ,已知
,已知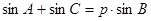 (
(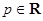 ),且
),且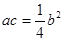 .
.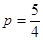 ,
,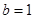 时,求
时,求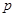 的取值范围.
的取值范围. 中,内角
中,内角 所对的边分别是
所对的边分别是 ,且
,且 .
. 的大小;
的大小; ,
,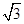 ,求
,求 的大小.
的大小.