题目内容
在△ABC中,a=3,b=2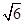 ,∠B=2∠A,
,∠B=2∠A,
(1)求cos A的值;
(2)求c的值.
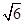 ,∠B=2∠A,
,∠B=2∠A,(1)求cos A的值;
(2)求c的值.
(1) (2)5
(2)5
 (2)5
(2)5(1)因为a=3,b=2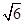 ,∠B=2∠A,
,∠B=2∠A,
所以在△ABC中,由正弦定理得 =
= .
.
所以 =
= .故cos A=
.故cos A= .
.
(2)由(1)知cos A= ,所以sin A=
,所以sin A= =
= .
.
又因为∠B=2∠A,所以cos B=2cos2A-1= .
.
所以sin B= =
= .
.
在△ABC中,sin C=sin(A+B)=sin Acos B+
cos Asin B= .
.
所以c= =5.
=5.
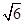 ,∠B=2∠A,
,∠B=2∠A,所以在△ABC中,由正弦定理得
 =
= .
.所以
 =
= .故cos A=
.故cos A= .
.(2)由(1)知cos A=
 ,所以sin A=
,所以sin A= =
= .
.又因为∠B=2∠A,所以cos B=2cos2A-1=
 .
.所以sin B=
 =
= .
.在△ABC中,sin C=sin(A+B)=sin Acos B+
cos Asin B=
 .
.所以c=
 =5.
=5.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
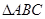 中,角A,B,C,的对边分别为
中,角A,B,C,的对边分别为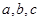 ,且
,且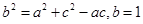
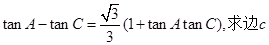 的值;
的值;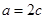 ,求
,求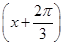 +2cos2
+2cos2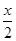 ,x∈R.
,x∈R.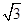 ,求a的值.
,求a的值.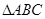 中,
中,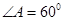 ,
,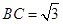 ,则
,则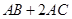 的最大值为 ;
的最大值为 ;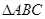 中,角
中,角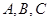 所对的边分别为
所对的边分别为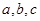 ,且
,且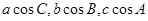 成等差数列.
成等差数列.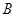 的大小;
的大小;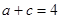 ,求
,求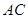 边上中线长的最小值.
边上中线长的最小值. 中,
中, ,
, ,
, 分别是角
分别是角 的对边.已知
的对边.已知 ,
, .
. ,求角
,求角 的大小;
的大小; ,求边
,求边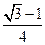 ,求C
,求C
 中,若
中,若 ,则
,则 .
.