题目内容
设△ABC的内角A,B,C所对的边分别为a,b,c,(a+b+c)(a-b+c)=ac
(1)求B
(2)若sinAsinC=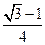 ,求C
,求C
(1)求B
(2)若sinAsinC=
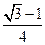 ,求C
,求C(1)120°
(2)15°或45°
(2)15°或45°
(1)∵(a+b+c)(a-b+c)=ac
∴a2+c2-b2=-ac
由余弦定理知cosB= =-
=-
∴B=120°
(2)由(1)知A+C=60°
∵cos(A-C)=cosAcosC+sinAsinC
= cosAcosC-sinAsinC+2sinAsinC
=cos(A+C)+2sinAsinC
= +
+ =
=
∴A-C=30°或A-C=-30°,∴C=15°或C=45°
∴a2+c2-b2=-ac
由余弦定理知cosB=
 =-
=-
∴B=120°
(2)由(1)知A+C=60°
∵cos(A-C)=cosAcosC+sinAsinC
= cosAcosC-sinAsinC+2sinAsinC
=cos(A+C)+2sinAsinC
=
 +
+ =
=
∴A-C=30°或A-C=-30°,∴C=15°或C=45°

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
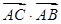 =4,求△ABC的面积S.
=4,求△ABC的面积S.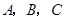 的三内角
的三内角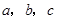 ,且
,且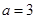 ,A=
,A=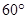 ,
,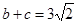 .
.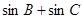 的值及
的值及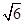 ,∠B=2∠A,
,∠B=2∠A, 中,角
中,角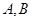 所对的边长分别为
所对的边长分别为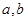 .若
.若
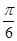


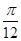
 c,当tan(A-B)取最大值时,角C的值为( )
c,当tan(A-B)取最大值时,角C的值为( )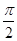
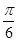


 .
. BAC=30o。BC为半圆的切线,且BC=4
BAC=30o。BC为半圆的切线,且BC=4 ,则点O到AC的距离OD= .
,则点O到AC的距离OD= .
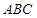 中,三个内角
中,三个内角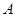 ,
,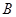 ,
,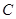 所对的边分别为
所对的边分别为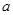 ,
,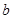 ,
,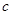 ,若
,若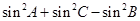
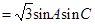 ,则
,则