题目内容
已知向量
表示“向东航行1km”，向量
表示“向南航行1km”，则向量
表示( )
A．向东南航行 km | B．向东南航行2km |
| C．向东北航行km | D．向东北航行2km |
A
解析试题分析：本题充分体现向量的大小和方向两个元素，根据实际意义知道两个向量的和向量方向是东南方向，大小可以用勾股定理做向量表示“向东航行1km”，向量表示“向南航行1km”， 由向量加法的几何意义知两个向量的和是向东南航行km，故选A．
考点：向量的加法几何意义
点评：本题考查向量的几何意义，大小和方向是向量的两个要素，分别是向量的代数特征和几何特征，借助于向量可以实现某些代数问题与几何问题的相互转化．
练习册系列答案
名师点拨卷系列答案
相关题目
已知
三个内角A，B，C所对的边，若
且
的面积
，则三角形的形状是（ ）
| A．等腰三角形 | B．等边三角形 |
| C．等腰直角三角形 | D．有一个为 的等腰三角形 |
中，点D在线段BC的延长线上，且
，点O在线段CD上（与点C,D不重合）若
则x的取值范围（ ）
给出下列命题：
（1）两个具有公共终点的向量，一定是共线向量。
（2）两个向量不能比较大小，但它们的模能比较大小。
（3）
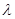a=0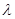（为实数），则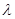必为零。
（4），
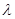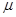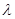为实数，若a=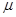b，则a与b共线。
其中错误的命题的个数为
| A．1 | B．2 | C．3 | D．4 |
已知
和点M满足
.若存在实数m使得
成立，则m= （ ）
| A．2 | B．3 | C．4 | D．5 |
设向量
，
，且
，则
等于
A． | B． | C． | D． |
已知平面向量
，
，且
，则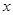
的值为（ ）
| A．－3 | B．-1 | C．1 | D．3 |
已知向量
，
，若
与
共线，则
等于（ ）
A． ； | B． | C． | D． |