题目内容
已知函数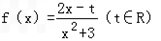
．
（1）若关于x的方程x2﹣tx﹣3=0的两实数为a，b（a＜b），试判断函数f（x）在区间（a，b）上的单调性，并说明理由；
（2）若函数f（x）的图象在x=﹣1处的切线斜率为
，求当x＞0时，f（x）的最大值．
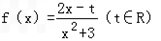．（1）若关于x的方程x2﹣tx﹣3=0的两实数为a，b（a＜b），试判断函数f（x）在区间（a，b）上的单调性，并说明理由；
（2）若函数f（x）的图象在x=﹣1处的切线斜率为
，求当x＞0时，f（x）的最大值．解：（1）∵
=
=
＞0
∴函数f（x）在区间（a，b）上的单调递增
（2）由（1）及已知可得，f'（﹣1）=
=
∴t=﹣2
当x＞0时，由f（x）
=
=
=
当且仅当x+1=
即x=1时取等号
∴f（x）的最大值为1
=
=
＞0∴函数f（x）在区间（a，b）上的单调递增
（2）由（1）及已知可得，f'（﹣1）=
=∴t=﹣2
当x＞0时，由f（x）
=
== 当且仅当x+1=
即x=1时取等号∴f（x）的最大值为1
练习册系列答案
单元加期末复习先锋大考卷系列答案
出彩同步大试卷系列答案
相关题目
元
，年销量为
万件，若已知
与
成正比，且售价为10元时，年销量为28万件。
关天
的图象关原点对称，
的图象在点P（1,m）处的切线的斜率为－6，且当x=2时
上是增函数，求n的取值范围.
）＞0