题目内容
4．若函数$f（x）=\left\{\begin{array}{l}{e^{x-1}}\;\;，\;\;x≤1\\ 5-{x^2}\;\;，\;\;x＞1\end{array}\right.$，则f（f（2））=（ ）| A． | 1 | B． | 4 | C． | 0 | D． | 5-e2 |
分析 由函数的解析式先求出f（2）的值，再求出f（f（2））的值．
解答 解：由题意知，$f（x）=\left\{\begin{array}{l}{{e}^{x-1}，x≤1}\\{5-{x}^{2}，x＞1}\end{array}\right.$，
则f（2）=5-4=1，f（1）=e0=1，
所以f（f（2））=1，
故选A．
点评 本题考查分段函数的函数值，对于多层函数值应从内到外依次求值，注意自变量的范围，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
14．某综艺节目为增强娱乐性，要求现场嘉宾与其场外好友连线互动．凡是拒绝表演节目的好友均无连线好友的机会；凡是选择表演节目的好友均需连线未参加过此活动的3个好友参与此活动，以此下去．
（Ⅰ）假设每个人选择表演与否是等可能的，且互不影响，则某人选择表演后，其连线的3个好友中不少于2个好友选择表演节目的概率是多少？
（Ⅱ）为调查“选择表演者”与其性别是否有关，采取随机抽样得到如表：
①根据表中数据，是否有99%的把握认为“表演节目”与好友的性别有关？
②将此样本的频率视为总体的概率，随机调查3名男性好友，设X为3个人中选择表演的人数，求X的分布列和期望．
附：K2=$\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$；
（Ⅰ）假设每个人选择表演与否是等可能的，且互不影响，则某人选择表演后，其连线的3个好友中不少于2个好友选择表演节目的概率是多少？
（Ⅱ）为调查“选择表演者”与其性别是否有关，采取随机抽样得到如表：
| 选择表演 | 拒绝表演 | 合计 | |
| 男 | 50 | 10 | 60 |
| 女 | 10 | 10 | 20 |
| 合计 | 60 | 20 | 80 |
②将此样本的频率视为总体的概率，随机调查3名男性好友，设X为3个人中选择表演的人数，求X的分布列和期望．
附：K2=$\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$；
| P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
12．在△ABC中，角A，B，C对应边分别为a，b，c，已知三个向量$\overrightarrow m=（a，cos\frac{A}{2}）$，$\overrightarrow n=（b，cos\frac{B}{2}）$，$\overrightarrow p=（c，cos\frac{C}{2}）$共线，则△ABC形状为（ ）
| A． | 等边三角形 | B． | 等腰三角形 | C． | 直角三角形 | D． | 等腰直角三角形 |
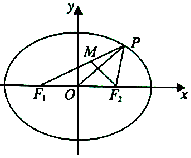如图所示，已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$，其中a＞b＞0，F1，F2分别为其左，右焦点，点P是椭圆C上一点，PO⊥F2M，且$\overrightarrow{{F_1}M}=λ\overrightarrow{MP}$．
9．已知函数$f（x）=lnx-x+\frac{1}{x}$，若$a=f（{\frac{1}{3}}）$，b=f（π），c=f（5），则（ ）
| A． | c＜b＜a | B． | c＜a＜b | C． | b＜c＜a | D． | a＜c＜b |
16．已知集合A={x|x2-9＞0}，B={x|2＜x≤5}，则A∩B=（ ）
| A． | （3，5] | B． | （-∞，-3）∪（5，+∞） | C． | （-∞，-3）∪[5，+∞） | D． | （-∞，2]∪（3，+∞） |
中国传统文化中很多内容体现了数学的对称美，如图所示的太极图是由黑白两个鱼形纹组成的圆形图案，充分展现了相互转化、对称统一的形式美、和谐美，给出定义：能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”，给出下列命题：