题目内容
设函数f(x)=
x2-(4+a)x+6ln(x+b),g(x)=5ln(x+b)+
x2-3x,函数f(x)在x=1与x=2处取得极值.
(1)求实数a、b的值;
(2)若φ(x)=f(x)-g(x),求证:当x∈(-1,+∞)时,φ(x)≤0恒成立;
(3)证明:若x>0,y>0,则xlnx+ylny≥(x+y)ln
.
| 1 |
| 2 |
| 1 |
| 2 |
(1)求实数a、b的值;
(2)若φ(x)=f(x)-g(x),求证:当x∈(-1,+∞)时,φ(x)≤0恒成立;
(3)证明:若x>0,y>0,则xlnx+ylny≥(x+y)ln
| x+y |
| 2 |
考点:利用导数研究函数的极值
专题:导数的综合应用
分析:(1)先求导函数,根据x=1与x=2是f(x)的一个极值点,可得f'(1)=0,f′(2)=0,从而可求a,b的值;
(2)先化简φ(x)=ln(x+1)-x,根据导数与最值的关系,求出φ(x)的最大值,即可得证
(3)利用(2)的结论,以及作差法比较即可
(2)先化简φ(x)=ln(x+1)-x,根据导数与最值的关系,求出φ(x)的最大值,即可得证
(3)利用(2)的结论,以及作差法比较即可
解答:
解:(1)∵f(x)=
x2-(4+a)x+6ln(x+b),
∴f′(x)=x-(4+a)+
,
∵函数f(x)在x=1与x=2处取得极值.
∴f′(1)=0,f′(2)=0,
∴
解得
,
(2)由(1)知,f(x)=
x2-4x+6ln(x+1),g(x)=5ln(x+1)+
x2-3x,
∴φ(x)=f(x)-g(x)=
x2-4x+6ln(x+1)-5ln(x+1)-
x2+3x=ln(x+1)-x
∴函数的定义域为(-1,+∞)
∴φ′(x)=
-1=
,
令φ′(x)=0,解得x=0,
当φ′(x)>0时,即-1<x<0时,函数φ(x)单调递增,
当φ′(x)<0时,即x>0时,函数φ(x)单调递减,
故当x=0时,函数φ(x)有极大值,φ(0)=0,
函数的极大值也是函数的最大值,
∴当x∈(-1,+∞)时,φ(x)≤0恒成立;
(3)证明:xlnx+ylny-(x+y)ln
=x(lnx-ln
)+y(lny-ln
)
=xln
+yln
,
=-xln
-ln
,
=-xln(1+
)-yln(1+
)
由(2)知,-xln(1+
)-yln(1+
)>-x•
-y•
=0
∴若x>0,y>0,则xlnx+ylny≥(x+y)ln
.
| 1 |
| 2 |
∴f′(x)=x-(4+a)+
| 6 |
| x+b |
∵函数f(x)在x=1与x=2处取得极值.
∴f′(1)=0,f′(2)=0,
∴
|
解得
|
(2)由(1)知,f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
∴φ(x)=f(x)-g(x)=
| 1 |
| 2 |
| 1 |
| 2 |
∴函数的定义域为(-1,+∞)
∴φ′(x)=
| 1 |
| x+1 |
| -x |
| x+1 |
令φ′(x)=0,解得x=0,
当φ′(x)>0时,即-1<x<0时,函数φ(x)单调递增,
当φ′(x)<0时,即x>0时,函数φ(x)单调递减,
故当x=0时,函数φ(x)有极大值,φ(0)=0,
函数的极大值也是函数的最大值,
∴当x∈(-1,+∞)时,φ(x)≤0恒成立;
(3)证明:xlnx+ylny-(x+y)ln
| x+y |
| 2 |
| x+y |
| 2 |
| x+y |
| 2 |
=xln
| 2x |
| x+y |
| 2y |
| x+y |
=-xln
| x+y |
| 2x |
| x+y |
| 2y |
=-xln(1+
| y-x |
| 2x |
| x-y |
| 2y |
由(2)知,-xln(1+
| y-x |
| 2x |
| x-y |
| 2y |
| y |
| 2x |
| x-y |
| 2y |
∴若x>0,y>0,则xlnx+ylny≥(x+y)ln
| x+y |
| 2 |
点评:本题主要考查利用导数研究函数的单调性、最值等知识及不等式恒成立问题的证明,考查分类讨论数学思想及转化划归思想的运用能力,属难题

练习册系列答案
相关题目
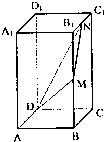 如图,在长方体ABCD-A1B1C1D1中,M、N分别为BB1、B1C1的中点,P为平面DMN内的一动点,若点P到平面BCC1B1的距离等于PD时,则点的轨迹是( )
如图,在长方体ABCD-A1B1C1D1中,M、N分别为BB1、B1C1的中点,P为平面DMN内的一动点,若点P到平面BCC1B1的距离等于PD时,则点的轨迹是( )| A、圆或圆的一部分 |
| B、抛物线的一部分 |
| C、双曲线的一部分 |
| D、椭圆的一部分 |