题目内容
已知中心在原点的焦点在坐标轴上的椭圆过点M(1,
),N(-
,
);求
(1)离心率e;
(2)椭圆上是否存在P(x,y)到定点A(a,0)(0<a<3)距离的最小值为1?若存在求a及P坐标,若不存在,说明理由.
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 2 |
| 2 |
(1)离心率e;
(2)椭圆上是否存在P(x,y)到定点A(a,0)(0<a<3)距离的最小值为1?若存在求a及P坐标,若不存在,说明理由.
考点:直线与圆锥曲线的关系,椭圆的应用
专题:圆锥曲线中的最值与范围问题
分析:(1)设椭圆方程为mx2+ny2=1(m>0,n>0,且m≠n),由椭圆过M,N两点,求出m,n得到椭圆的方程,即得离心率;
(2)设存在点P(x,y)满足条件,根据椭圆的方程,列出目标式|AP|2,求出满足条件的最值即可.
(2)设存在点P(x,y)满足条件,根据椭圆的方程,列出目标式|AP|2,求出满足条件的最值即可.
解答:
解:(1)设椭圆方程为mx2+ny2=1(m>0,n>0,且m≠n),
∵椭圆过M,N两点,
∴
,
解得
,
∴椭圆的方程为
+
=1,
∴离心率为e=
=
=
;
(2)设存在点P(x,y)满足题设条件,
由椭圆方程为
+
=1,得y2=4(1-
);
∴|AP|2=(x-a)2+y2
=(x-a)2+4(1-
)
=
(x-
a)2+4-
a2(|x|≤3),
当|
a|≤3,即0<a≤
时,|AP|2的最小值为4-
a2;
令4-
a2=1,解得a=±
∉(0,
];
∴
a>3,即
<a<3,此时当x=3时,|AP|2的最小值为(3-a)2;
令(3-a)2=1,解得a=2,此时点P的坐标是(3,0);
∴当a=2时,存在这样的点P满足条件,且P点的坐标是(3,0).
∵椭圆过M,N两点,
∴
|
解得
|
∴椭圆的方程为
| x2 |
| 9 |
| y2 |
| 4 |
∴离心率为e=
| c |
| a |
| ||
| 3 |
| ||
| 3 |
(2)设存在点P(x,y)满足题设条件,
由椭圆方程为
| x2 |
| 9 |
| y2 |
| 4 |
| x2 |
| 9 |
∴|AP|2=(x-a)2+y2
=(x-a)2+4(1-
| x2 |
| 9 |
=
| 5 |
| 9 |
| 9 |
| 5 |
| 4 |
| 5 |
当|
| 9 |
| 5 |
| 5 |
| 3 |
| 4 |
| 5 |
令4-
| 4 |
| 5 |
| ||
| 2 |
| 5 |
| 3 |
∴
| 9 |
| 5 |
| 5 |
| 3 |
令(3-a)2=1,解得a=2,此时点P的坐标是(3,0);
∴当a=2时,存在这样的点P满足条件,且P点的坐标是(3,0).
点评:本题考查了椭圆与直线的位置关系的应用问题,也考查了求最值问题,解题时应注意灵活运用公式解答问题,是中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
函数f(x)=ax3+(a-1)x2+48(a-2)x+b的图象关于原点成中心对称图形,则f(x)在[-4,4]上的单调性是( )
| A、[-4,0]上是增函数[0.4]上是减函数 |
| B、增函数 |
| C、减函数 |
| D、不具备单调性 |
已知
、
、
是不共面的三个向量,则下列向量组能作为一个基底的是( )
| a |
| b |
| c |
A、2
| ||||||||||
B、2
| ||||||||||
C、
| ||||||||||
D、
|
 在四棱锥P-ABCD中,∠ABC═∠ACD=90°,∠BAC=∠CAD=60°,PA⊥底面ABCD,E为PD的中点,PA=2AB=2.
在四棱锥P-ABCD中,∠ABC═∠ACD=90°,∠BAC=∠CAD=60°,PA⊥底面ABCD,E为PD的中点,PA=2AB=2.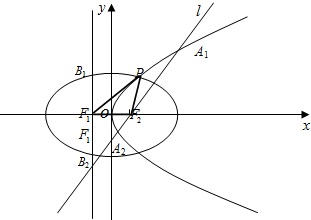 如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1、F2为焦点,离心率e=
如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1、F2为焦点,离心率e=