题目内容
11.如图1,将水平放置且边长为1的正方形ABCD沿对角线BD折叠,使C到C′位置.折叠后三棱锥C′-ABD的俯视图如图2所示,那么其主视图是( )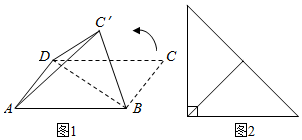
| A. | 等边三角形 | B. | 直角三角形 | ||
| C. | 两腰长都为$\frac{{\sqrt{3}}}{2}$的等腰三角形 | D. | 两腰长都为$\frac{{\sqrt{2}}}{2}$的等腰三角形 |
分析 根据三棱锥的俯视图确定三棱锥的主视图,根据主视图的结构计算腰长即可.
解答  解:由俯视图可知,平面C′BD⊥平面ABD,则其主视图如图所示,
解:由俯视图可知,平面C′BD⊥平面ABD,则其主视图如图所示,
则为等腰三角形.其腰长为$\sqrt{(\frac{1}{2})^{2}+(\frac{\sqrt{2}}{2})^{2}}$=$\frac{\sqrt{3}}{2}$,
故选:C.
点评 本题主要考查三视图的识别和应用,根据三棱锥的结构得到三棱锥的主视图是解决本题的关键.

练习册系列答案
相关题目
 如图,在长方体ABCD-A1B1C1D1中,点P是棱CD上一点,则三棱锥P-A1B1A的左视图可能为( )
如图,在长方体ABCD-A1B1C1D1中,点P是棱CD上一点,则三棱锥P-A1B1A的左视图可能为( )


