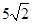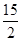题目内容
已知对于任意 ,都有
,都有 ,且
,且 ,则
,则 是( )
是( )
| A.奇函数 | B.偶函数 |
| C.奇函数且偶函数 | D.非奇且非偶函数 |
B
解析试题分析:令x=y得f(x)+f(x)=2f(x)f(0),∴f(0)=1,令y=-x得f(x)+f(-x)=2f(x)f(0)=2f(x),∴f(x)="f(-x)" ,∴函数f(x)为偶函数
考点:本题考查了抽象函数的性质
点评:赋值法是解决抽象函数的单调性的运用。

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
下列函数在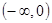 上是增函数的是( )
上是增函数的是( )
A.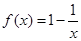 | B.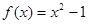 | C. | D.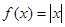 |
已知函数 ( )
( )
A. | B. | C. | D. |
函数 的最大值是( )
的最大值是( )
A. | B. | C. | D. |
函数 的值域是( )
的值域是( )
A. | B. | C. | D. |
已知 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
已知函数 ,在区间
,在区间 内存在
内存在 使
使 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
已知函数
 ,则函数( )
,则函数( )
A.是奇函数,在 上是减函数 上是减函数 |
B.是偶函数,在 上是减函数 上是减函数 |
C.是奇函数,在 上是增函数 上是增函数 |
D.是偶函数,在 上是增函数 上是增函数 |
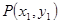 、
、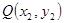 之间的“理想距离”为:
之间的“理想距离”为: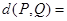
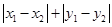 ;若
;若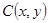 到点
到点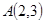 、
、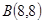 的“理想距离”相等,其中实数
的“理想距离”相等,其中实数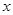 、
、 满足
满足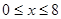 、
、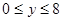 ,则所有满足条件的点
,则所有满足条件的点 的轨迹的长度之和是
的轨迹的长度之和是