题目内容
在平面直角坐标系中,定义点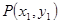 、
、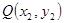 之间的“理想距离”为:
之间的“理想距离”为: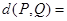
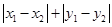 ;若
;若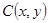 到点
到点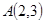 、
、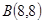 的“理想距离”相等,其中实数
的“理想距离”相等,其中实数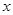 、
、 满足
满足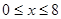 、
、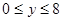 ,则所有满足条件的点
,则所有满足条件的点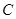 的轨迹的长度之和是
的轨迹的长度之和是
A.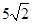 | B.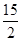 | C.10 | D.5 |
D
解析试题分析:由新定义得,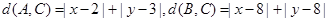 ,由
,由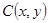 到点
到点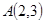 、
、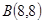 的“理想距离”相等,得
的“理想距离”相等,得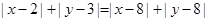 …………(1)
…………(1)
当y≥8时,(1)化为|x-2|+5=|x-8|,无解;
当y≤3时,(1)化为|x-2|=5+|x-8|,无解;
当3≤y≤8时,(1)化为2y-11=|x-8|-|x-2|,y=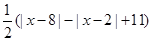 其图象如图所示。
其图象如图所示。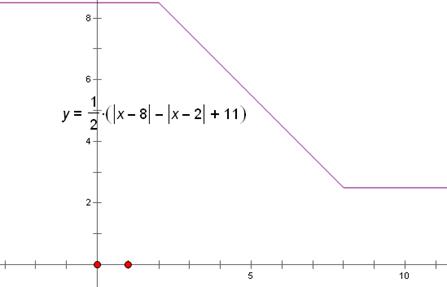
若x≤2,则y=8.5,不在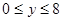 内;
内;
若2≤x≤8,则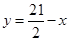 ,线段端点为(2.5,8),(7.5,3),线段长度为
,线段端点为(2.5,8),(7.5,3),线段长度为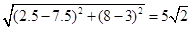 ;
;
若x≥8,则y=2.5,不在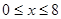 内。
内。
综上可知,点C的轨迹构成的线段长度之和为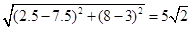 。选A。
。选A。
考点:本题主要考查学习能力,轨迹的概念,分类讨论思想,距离计算。
点评:新定义问题,近几年高考中,这种“新定义问题”屡见不鲜,难题易题均有,关键是要理解给出的新信息。分类讨论,细心计算。

练习册系列答案
相关题目
已知定义域为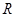 的函数
的函数 满足
满足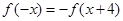 ,则
,则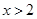 时,
时, 单调递增,若
单调递增,若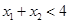 ,且
,且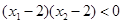 ,则
,则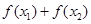 与0的大小关系是( )
与0的大小关系是( )
A.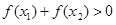 | B.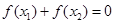 |
C. | D.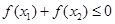 |
已知函数 f(x)的定义域为 ,其导函数f'(x)的图象如图所示,则对于任意
,其导函数f'(x)的图象如图所示,则对于任意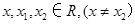 ,下列结论正确的是( )
,下列结论正确的是( )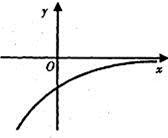
①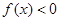 恒成立;
恒成立;
②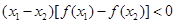 ;
;
③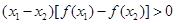 ;
;
④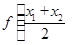 >
> 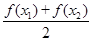 ;
;
⑤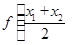 <
< 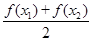 .
.
| A.①③ | B.①③④ | C.②④ | D.②⑤ |
设函数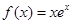 ,则( )
,则( )
A.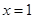 为 为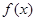 的极大值点 的极大值点 | B.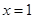 为 为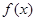 的极小值点 的极小值点 |
C.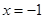 为 为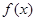 的极大值点 的极大值点 | D.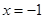 为 为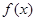 的极小值点 的极小值点 |
已知对于任意 ,都有
,都有 ,且
,且 ,则
,则 是( )
是( )
| A.奇函数 | B.偶函数 |
| C.奇函数且偶函数 | D.非奇且非偶函数 |
函数 在实数集上是增函数,则
在实数集上是增函数,则
A.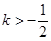 | B. | C. | D. |
设函数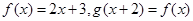 ,则
,则 的表达式是( )
的表达式是( )
A.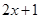 | B.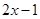 | C.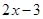 | D.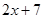 |
为了求函数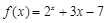 的一个零点,某同学利用计算器得到自变量
的一个零点,某同学利用计算器得到自变量 和函数
和函数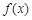 的部分对应值,如表所示:
的部分对应值,如表所示:
 | 1.25 | 1.3125 | 1.375 | 1.4375 | 1.5 | 1.5625 |
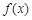 | -0.8716 | -0.5788 | -0.2813 | 0.2101 | 0.32843 | 0.64115 |
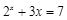 的近似解(精确到0.1)可取为
的近似解(精确到0.1)可取为(A)1.32 (B)1.39 (C)1.4 (D)1.3
对于函数f (x)和g(x),其定义域为[a, b],若对任意的x∈[a, b]总有|1- |≤
|≤ ,则称f (x)可被g(x)置换,那么下列给出的函数中能置换f (x)=
,则称f (x)可被g(x)置换,那么下列给出的函数中能置换f (x)= x∈[4,16]的是 ( )
x∈[4,16]的是 ( )
| A.g(x)=2x+6 x∈[4,16] | B.g(x)=x2+9 x∈[4,16] |
C.g(x)=  (x+8) x∈[4,16] (x+8) x∈[4,16] | D.g(x)= (x+6) x∈[4,16] (x+6) x∈[4,16] |